そまちょブログのそまちょ(@somachob)です。
この記事は、Sky株式会社プログラミングコンテスト2023(AtCoder Beginner Contest 289)のB問題についての解説です。
A問題については、こちらの記事で解説しています。
競技プログラミングって何?って方はこちらの記事を見てみてください。
B – レ
■問題文
1 から N までの N 個の整数が小さい順に並んでいます。
整数の間に M 個の「レ」が挟まっています。i 個目の「レ」は、整数 ai と整数 ai + 1 の間にあります。
N 個の整数を1回ずつ全て読みます。
B – レ
- まず、N 頂点 M 辺の無向グラフ G を考える。i 本目の辺は頂点 ai と頂点 ai + 1 を結んでいる。
- そして、読まれていない整数がなくなるまで、次の操作を繰り返す。
- 読まれていない整数のうち最小のものを x として、頂点 x が含まれる連結成分 C を選び、C に含まれる頂点の番号を大きい方から順にすべて読む。
例として示されている、N = 5、M = 3、a = (1, 3, 4) では、次のようになります。
それぞれの連結成分について、反転させて出力させます。
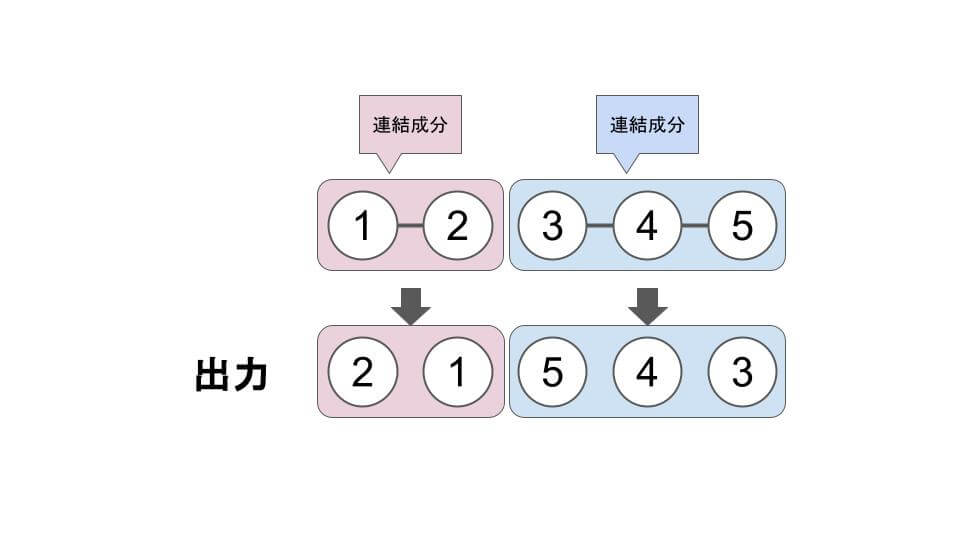
最小の x から、どこの整数までつながっているかを考えるのが大事になります。
いろいろな解答をご紹介します。
繰り返しを工夫する
for 文を使った解答コードです。
#include <bits/stdc++.h>
using namespace std;
int main () {
// 入力
int n, m;
cin >> n >> m;
// つながっているかを管理する変数
vector<bool> v(n + 1, false);
for(int i = 0; i < m; i++) {
int a;
cin >> a;
v[a] = true; // つながっている
}
// 1 から n まで繰り返し
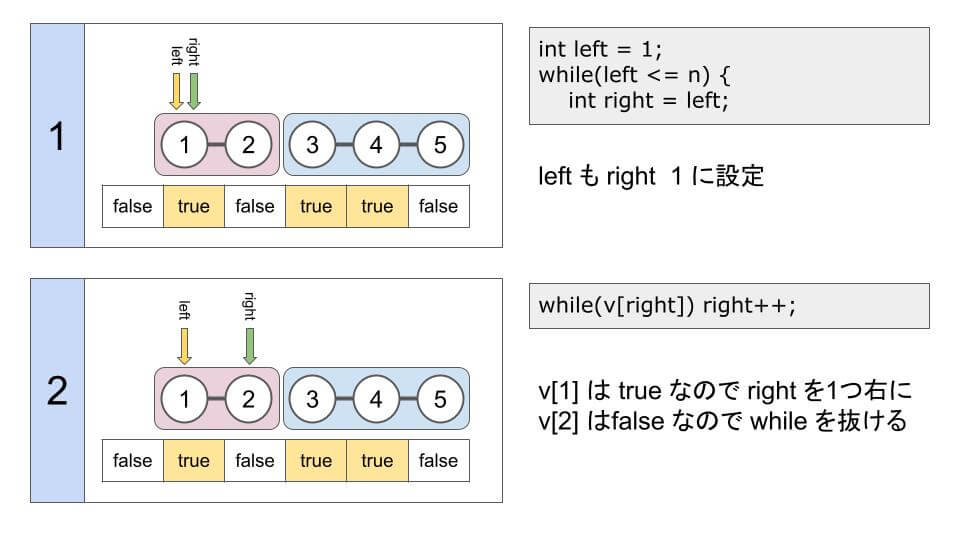
int left = 1;
while(left <= n) {
// 連結成分の一番大きい値
int right = left;
// つながっている場合は右にずらす
while(v[right]) right++;
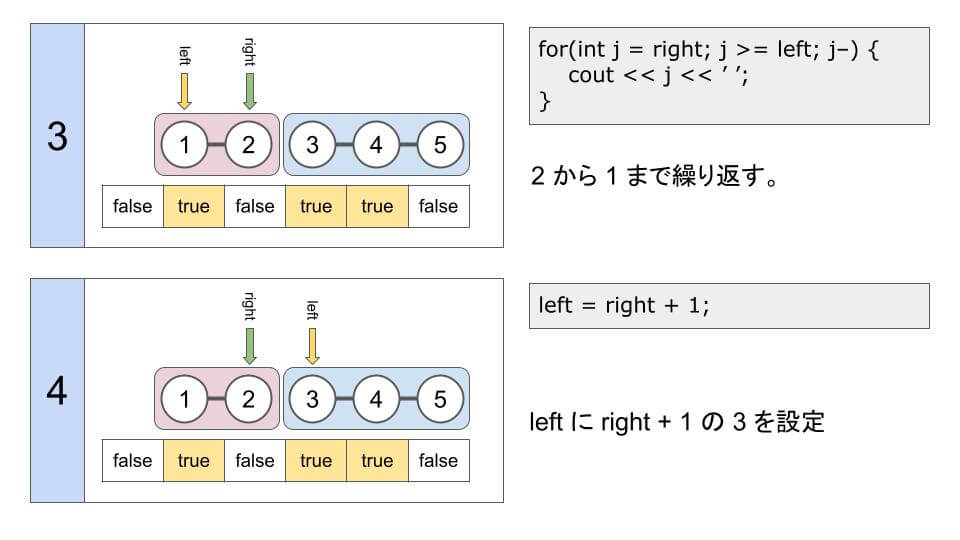
// 右の値から左の値まで順に出力
for(int j = right; j >= left; j--) {
cout << j << ' ';
}
// 次の連結成分に移動
left = right + 1;
}
return 0;
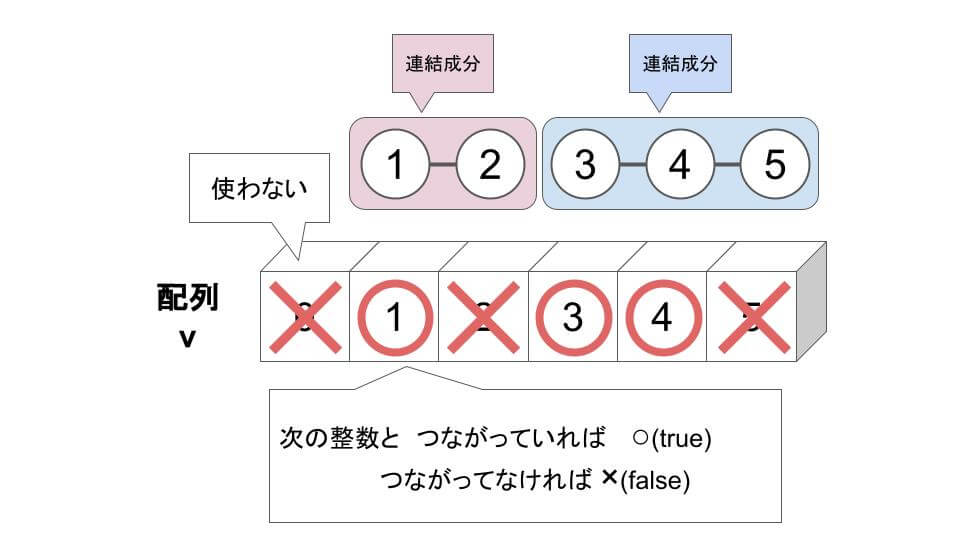
}整数が次の整数とつながっているかを、配列 v で管理しています。
vector は、次のように宣言すれば、すべての要素に同じ値を設定できます。
vector<型> 変数名(要素数, 値)vector<bool> v(n + 1, false);
for(int i = 0; i < m; i++) {
int a;
cin >> a;
v[a] = true; // つながっている
}N = 5、M = 3、a = (1, 3, 4) では、次のようになります。
vector<bool> は、すべての要素が false で初期化されるので、「vector v(n + 1, false);」 とせずに 「vector<bool> v(n + 1);」 でも問題ありません。
出力するためのメインのコードが以下の部分です。
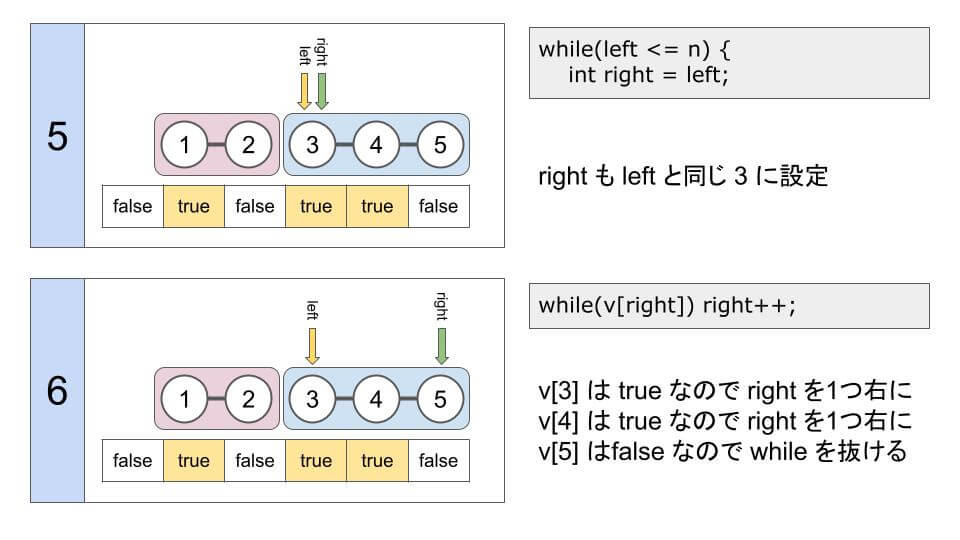
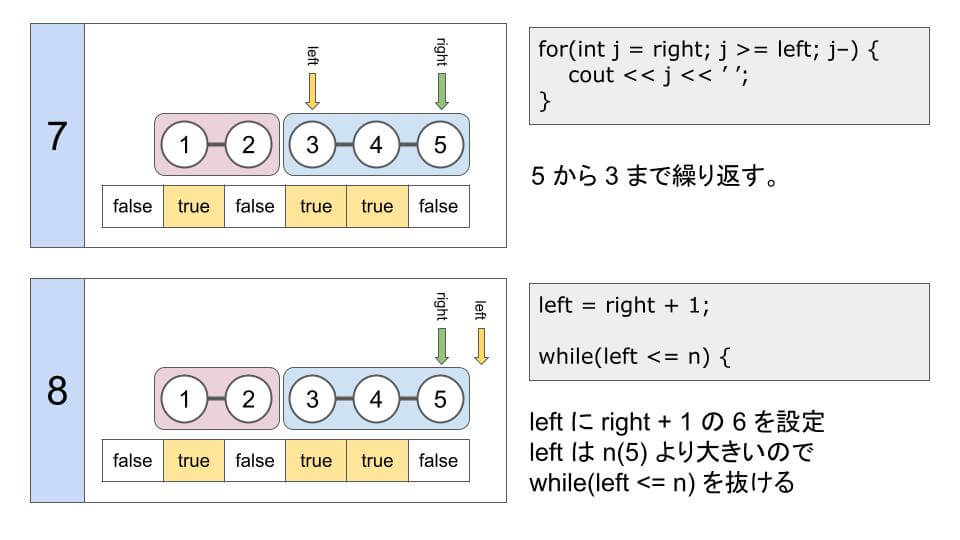
int left = 1;
while(left <= n) {
// 連結成分の一番大きい値
int right = left;
// つながっている場合は右にずらす
while(v[right]) right++;
// 右の値から左の値まで順に出力
for(int j = right; j >= left; j--) {
cout << j << ' ';
}
// 次の連結成分に移動
left = right + 1;
}N = 5、M = 3、a = (1, 3, 4) では、次のようになります。
配列 v は、要素 (1, 3, 4) が true になるので v = {false, true, false, true, true, false}になります。
Union-Find を使う
グループ分けを効率的に管理できる Union-Find を使った解答コードです。
#include <bits/stdc++.h>
using namespace std;
struct UnionFind {
// 親の要素とサイズを管理する変数
vector<int> parent, size;
// 変数の初期化
UnionFind(int n) : parent(n, -1), size(n, 1) {}
// x の根を求める
int root(int x) {
// x が根のとき
if(parent[x] == -1) return x;
// 経路圧縮
return parent[x] = root(parent[x]);
}
// x と y の根が同じか
bool isSame(int x, int y) {
return root(x) == root(y);
}
// x と y のグループを併合する
void unite(int x, int y) {
// x と y の根を取得
int rootX = root(x);
int rootY = root(y);
// x と y が同じグループのときは何もしない
if (rootX == rootY) return;
// union by size( y のサイズが小さくなるように調整 )
if (size[rootX] < size[rootY]) swap(rootX, rootY);
// y の親を x にする
parent[rootY] = rootX;
// x のサイズに y のサイズを足す
size[rootX] += size[rootY];
}
// x のサイズを取得
int getSize(int x) {
return size[root(x)];
}
};
int main () {
// 入力
int n, m;
cin >> n >> m;
// UnionFind の宣言
UnionFind uf(n + 1);
for(int i = 0; i < m; i++) {
int a;
cin >> a;
uf.unite(a, a + 1); // グループを併合する
}
// 1 から n まで繰り返し
int left = 1;
while(left <= n) {
// 連結成分の一番大きい値
int right = left + uf.getSize(left) - 1;
// 右の値から左の値まで順に出力
for(int j = right; j >= left; j--) {
cout << j << ' ';
}
// 次の連結成分に移動
left = right + 1;
}
return 0;
}Union-Find については、こちらの記事で解説しています。
Union-Find を使えば、同じ連結成分かどうか、連結成分のサイズ(要素の数)が簡単に取得できます。
基本的な考え方は、「繰り返しを工夫する」のコードと同じです。
連結成分の一番大きい値を取得する方法が異なります。
Union-Find を使うことで連結成分のサイズを取得して、left に足すことで連結成分の一番大きい値を求めています。
int right = left + uf.getSize(left) - 1;stack を使う
stack を使った解答コードです。
#include <bits/stdc++.h>
using namespace std;
int main () {
// 入力
int n, m;
cin >> n >> m;
// つながっているかを管理する変数
vector<bool> v(n + 1, false);
for(int i = 0; i < m; i++) {
int a;
cin >> a;
v[a] = true; // つながっている
}
stack<int> s; // 連結成分を積むstack
// 1 から n まで繰り返し
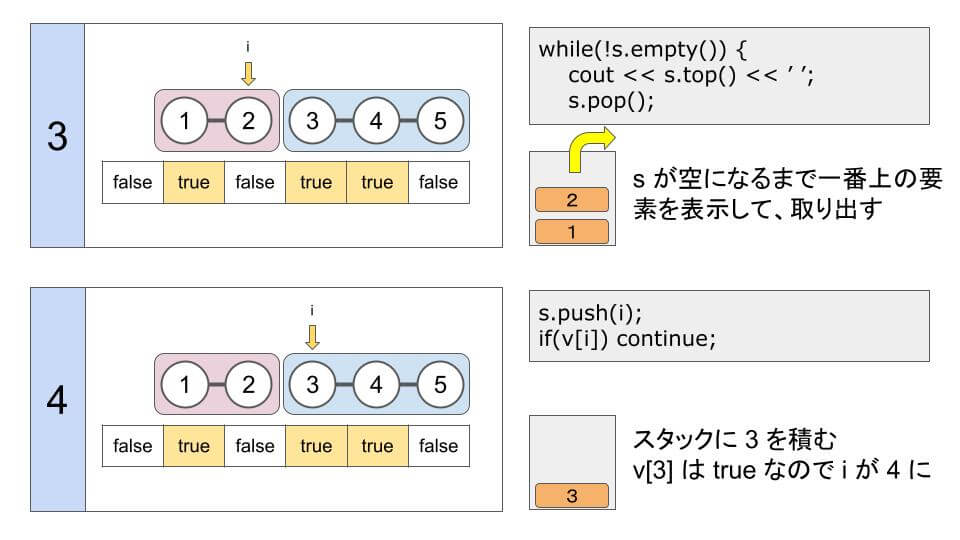
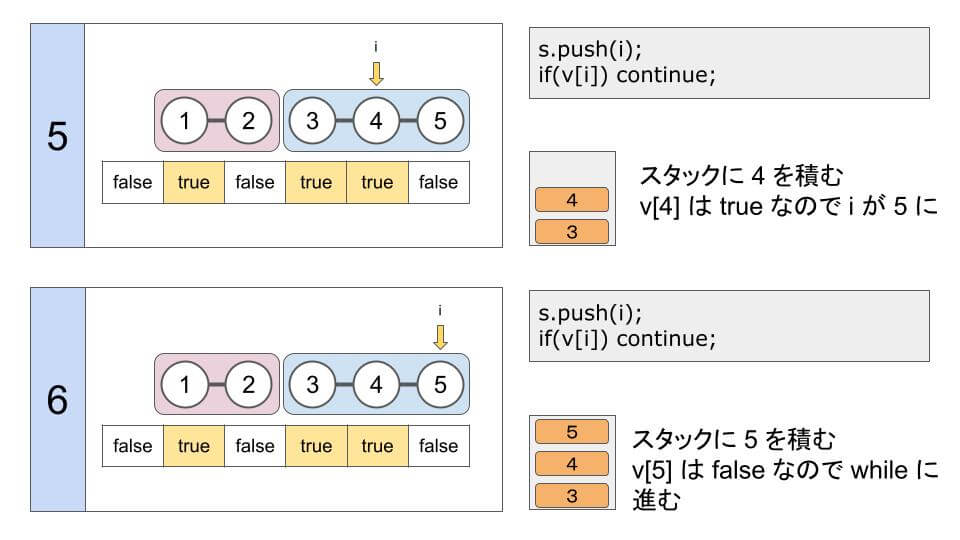
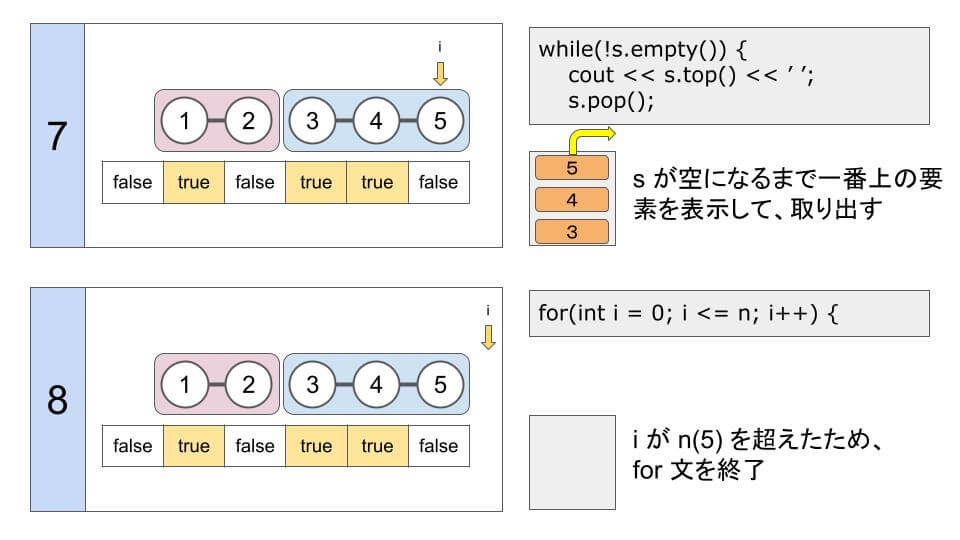
for(int i = 1; i <= n; i++) {
s.push(i); // stack に積む
if(v[i]) continue; // 連結されているので次の整数に
// stack が空になるまで繰り返す
while(!s.empty()) {
cout << s.top() << ' '; // 一番上の要素を出力
s.pop(); // 一番上の要素を取り出す
}
}
return 0;
}stack は、新しく追加したものを先に取り出すデータ構造です。
top は、一番上の要素をさします。push で、一番上に要素を積みます。popで、一番上の要素を取り出します。
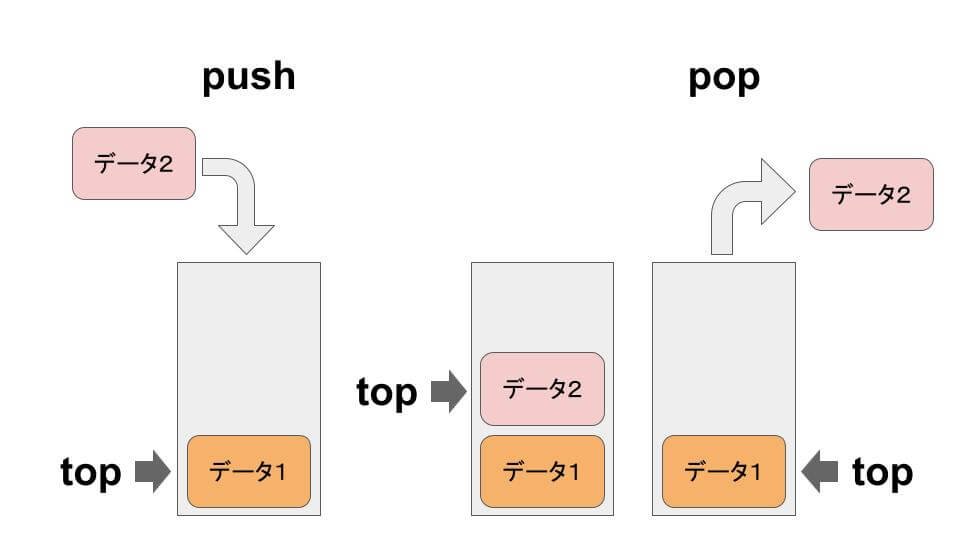
- S.push(x):S の一番上に要素 x を追加する。
- S.top():S の一番上の要素を取得する。
- S.pop():S の一番上の要素を削除する。
- S.empty():S が空かどうかを返す。
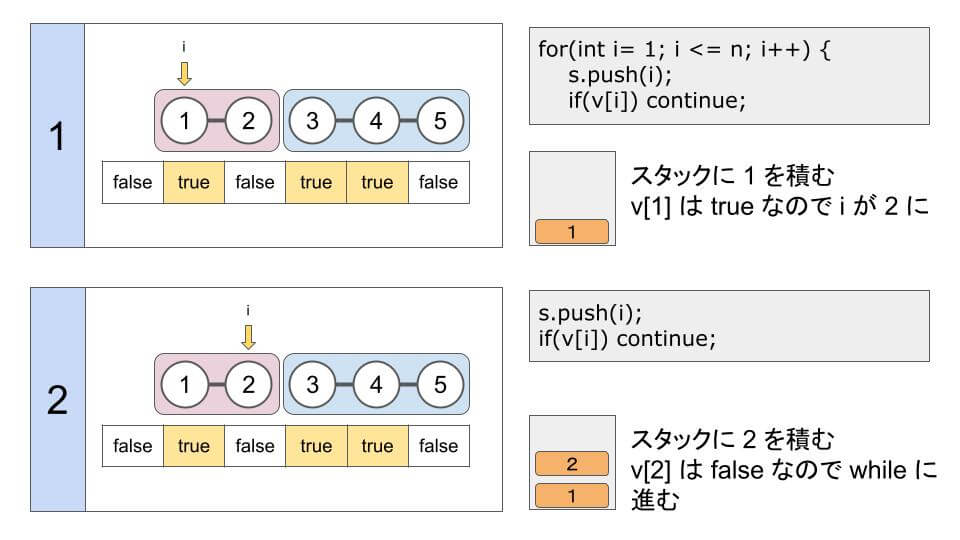
出力するためのメインとなるコードが次の部分です。
// 1 から n まで繰り返し
for(int i = 1; i <= n; i++) {
s.push(i); // stack に積む
if(v[i]) continue; // 連結されているので次の整数に
// stack が空になるまで繰り返す
while(!s.empty()) {
cout << s.top() << ' '; // 一番上の要素を出力
s.pop(); // 一番上の要素を取り出す
}
}N = 5、M = 3、a = (1, 3, 4) では、次のようになります。
反転させる
解説放送での解答コードです。連結成分の区切り位置を管理して、連結成分ごとに反転させます。
#include <bits/stdc++.h>
using namespace std;
int main () {
// 入力
int n, m;
cin >> n >> m;
// つながっているかを管理する変数
vector<bool> re(n + 1);
for(int i = 0; i < m; i++) {
int a;
cin >> a;
re[a] = true; // つながっている
}
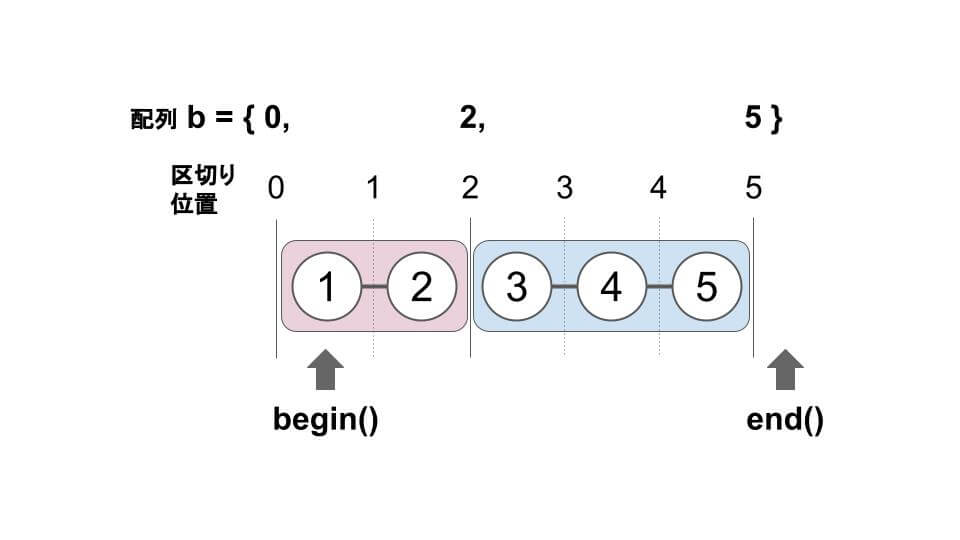
// 区切り位置を管理する変数
vector<int> b;
for(int i = 0; i <= n; i++) {
if(!re[i]) b.push_back(i); // 区切り位置を追加
}
// 答えの変数
vector<int> answer;
for(int i = 1; i <= n; i++) answer.push_back(i); // 1 から n までを代入
// 区切位置ごとに反転
for(int i = 0; i < b.size() - 1; i++) {
reverse(answer.begin() + b[i], answer.begin() + b[i + 1]);
}
// 答えの出力
for(auto i : answer) cout << i << ' ' ;
return 0;
}vector は、push_back(x) を使えば、新しい要素 x を配列の末尾に追加できます。
#include <bits/stdc++.h>
using namespace std;
int main () {
vector<int> v = {0, 1, 2};
v.push_back(3); // => 末尾に 3 が追加される。
// v = {0, 1, 2, 3} になる
return 0;
}reverse は、要素の並びを反転できます。要素の範囲を指定することで、配列の一部を反転させることもできます。
begin は、配列の先頭のイテレータを取得します。
N = 5、M = 3、a = (1, 3, 4) において、区切り位置と配列 b は、次のようになります。
#include <bits/stdc++.h>
using namespace std;
int main () {
vector<int> v1 = {1, 2, 3, 4, 5};
reverse(v1.begin(), v1.end()); // => v1 = {5, 4, 3, 2, 1}
vector<int> v2 = {1, 2, 3, 4, 5};
reverse(v2.begin(), v2.begin() + 2); // => v2 = {2, 1, 3, 4, 5}
vector<int> v3 = {1, 2, 3, 4, 5};
reverse(v3.begin() + 2, v3.begin() + 5); // => v3 = {1, 2, 5, 4, 3}
return 0;
}答えを出力しているのが次のコードです。範囲 for 文を使って配列 answer の値を出力しています。
// 答えの出力
for(auto i : answer) cout << i << ' ' ;範囲 for 文は、次のように書きます。auto は、変数の型を推論してくれます。
for (型 要素1つ分の変数名 : 処理したい変数)再帰関数を使う
再帰関数を使った解答コードです。
#include <bits/stdc++.h>
using namespace std;
vector<bool> v, read;
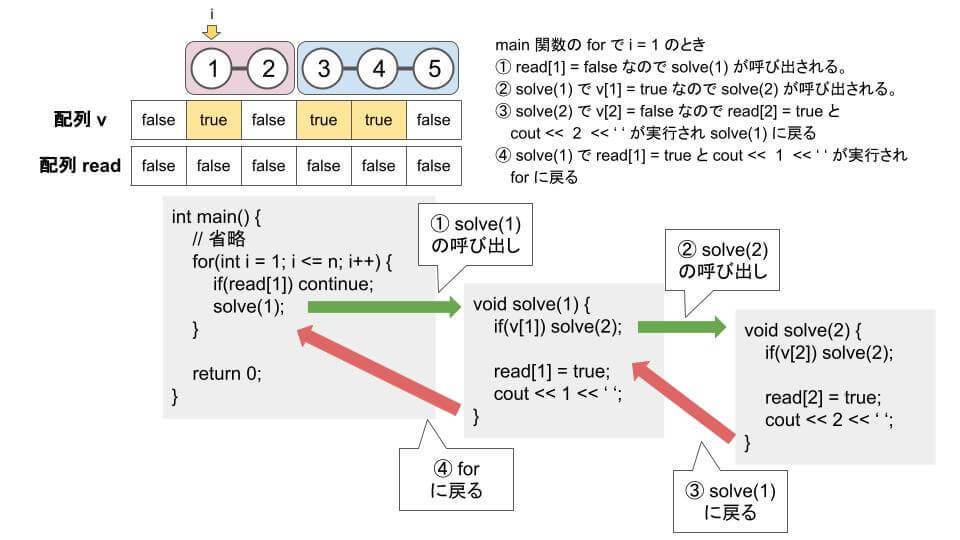
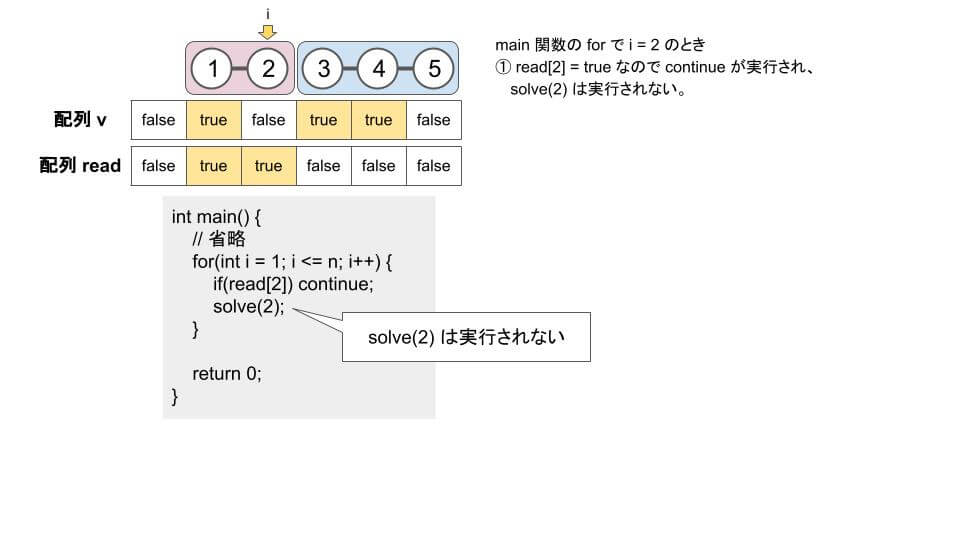
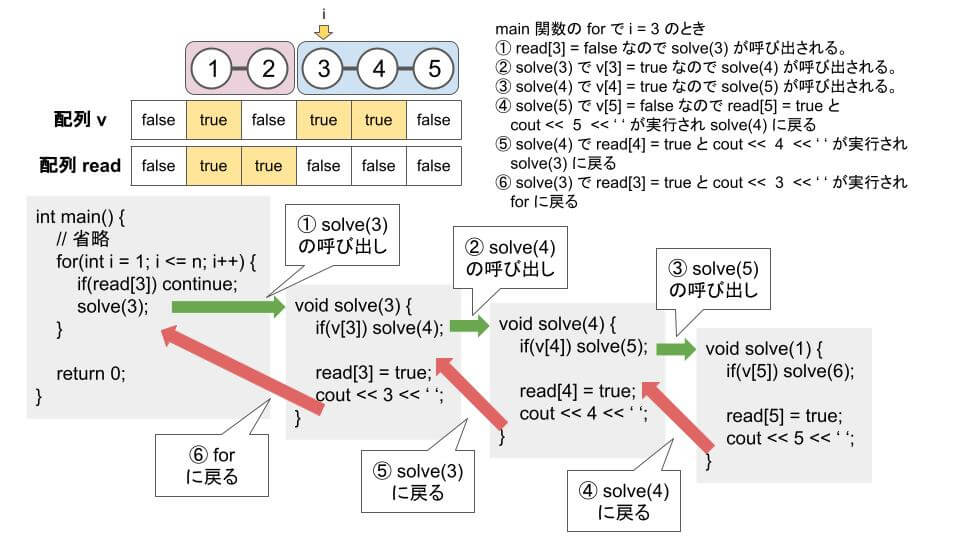
void solve(int i) {
if(v[i]) solve(i + 1); // つながっているときは 1 つ先に
read[i] = true; // i を読んだことにする
cout << i << ' ';
}
int main () {
// 入力
int n, m;
cin >> n >> m;
// つながっているかを管理する変数
v.assign(n + 1, false);
for(int i = 0; i < m; i++) {
int a;
cin >> a;
v[a] = true; // つながっている
}
// 読んでいるかを管理する変数
read.assign(n + 1, false);
// 1 から n まで繰り返し
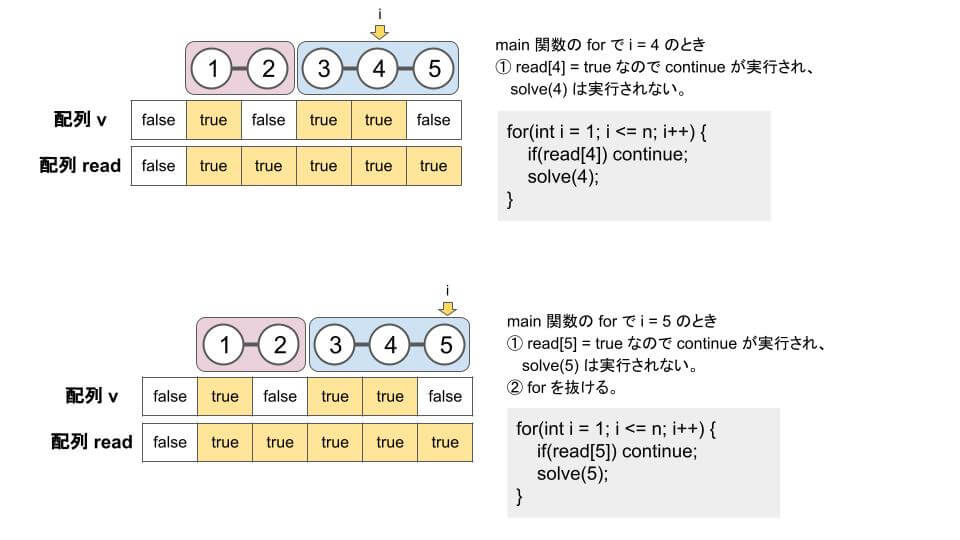
for(int i = 1; i <= n; i++) {
if(read[i]) continue; // すでに読んでいる
solve(i);
}
return 0;
}solve を再帰関数として実装しています。
void solve(int i) {
if(v[i]) solve(i + 1); // つながっているときは 1 つ先に
read[i] = true; // i を読んだことにする
cout << i << ' ';
}つながっているかを管理する変数 v と読んだかを管理する read は、main 関数と solve 関数からアクセスしたいので、グローバル変数にしています。
assign は、vector を指定した値で再代入します。
v.assign(n, t); // 要素数 n で、すべての値を t に N = 5、M = 3、a = (1, 3, 4) では、次のようになります。
グラフ を使う
深さ優先探索での解答コードです。
#include <bits/stdc++.h>
using namespace std;
using Graph = vector<vector<int>>;
Graph g;
vector<bool> seen;
// 深さ優先探索
void dfs(int v) {
seen[v] = true; // v を訪問済みにする
// v から行ける各頂点 next_v について
for(auto next_v : g[v]) {
if(seen[next_v]) continue; // next_v が探索済みなら探索しない
dfs(next_v); // 再帰的に探索
}
cout << v << ' ';
}
int main () {
// 入力
int n, m;
cin >> n >> m;
// グラフ入力
g.resize(n + 1);
for(int i = 0; i < m; i++) {
int a;
cin >> a;
g[a].push_back(a + 1); // 有向グラフ
}
// 訪問済みかを管理する変数
seen.assign(n, false);
// 1 から n まで繰り返し
for(int i = 1; i <= n; i++) {
if(seen[i]) continue; // すでに訪問済み
dfs(i); // 深さ優先探索
}
return 0;
}グラフは、2次元配列でデータを管理します。
using Graph = vector<vector<int>>;
Graph g;N = 5、M = 3、a = (1, 3, 4) では、次のようになります。
g[1] = {2}
g[2] = {}
g[3] = {4}
g[4] = {5}
g[5] = {}再帰関数のときのように、グラフ g と訪問済みかを管理する seen はグローバル変数にしています。
resize は、vector の要素数を変更します。
g.resize(n); // 要素数 n に変更するdfs 関数内では、範囲 for 文を使って繰り返しています。
// v から行ける各頂点 next_v について
for(auto next_v : g[v]) {
if(seen[next_v]) continue; // next_v が探索済みなら探索しない
dfs(next_v); // 再帰的に探索
}参考
DFS (深さ優先探索) 超入門! 〜 グラフ・アルゴリズムの世界への入口 〜【前編】 – Qiita
競技プログラミングの勉強におすすめの書籍を紹介します。



