幅優先探索って何？Pythonで学ぶ初心者向け入門ガイド

競技プログラミングをする上で、探索アルゴリズムを理解するのは重要です。

探索アルゴリズムの有名なものに、深さ優先探索と幅優先探索があります。

幅優先探索は、最短経路を求めたいときに特に活躍するアルゴリズムです。

この記事では、競技プログラミング初心者に向けて、幅優先探索についてわかりやすく解説します。

幅優先探索の基礎知識
1. 幅優先探索とは？
2. キューとの関係性
幅優先探索の基本コード
問題を解いてみる
参考

幅優先探索の基礎知識

幅優先探索とは？

幅優先探索は、グラフや木などのデータを探索するアルゴリズムの１つです。

幅優先探索（BFS：Breadth-First Search）と深さ優先探索（DFS：Depth-First Search）は、探索する順番がちがいます。

幅優先探索：探索を始めるところから近い順に探索する。
深さ優先探索：進めなくなる深いところまで探索する。

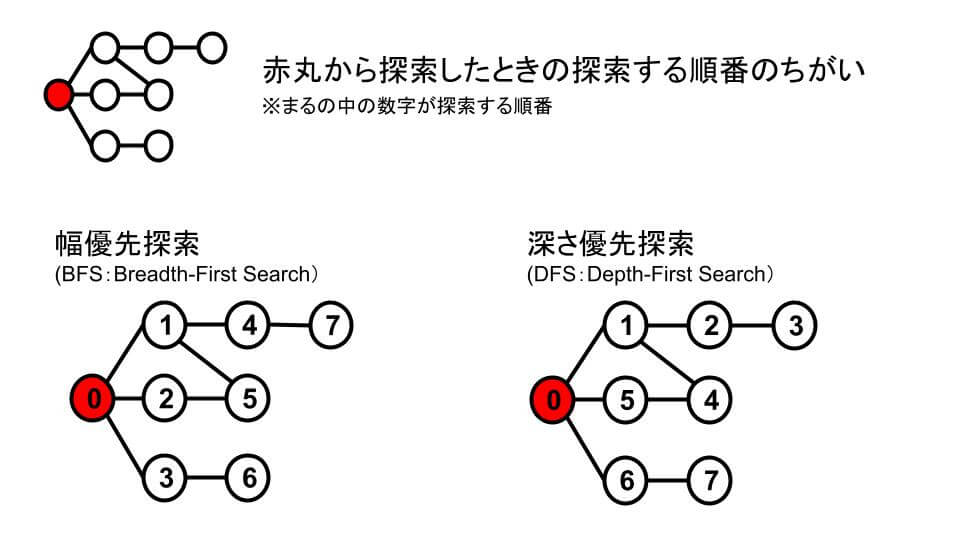
幅優先探索は、開始地点から１回でたどりつけるところを探索→２回でたどりつけるところを探索→３回でたどりつけるところを探索→・・・・という順番で探索していきます。

幅優先探索は、探索を始めるところから近い順に探索するので、最短距離を求めるのに適しています。

先ほどの図で、幅優先探索がどのように探索するかを説明します。

わかりやすいように開始地点を０として、それ以外の地点について A ~ G のアルファベットを振っています。

ステップ１

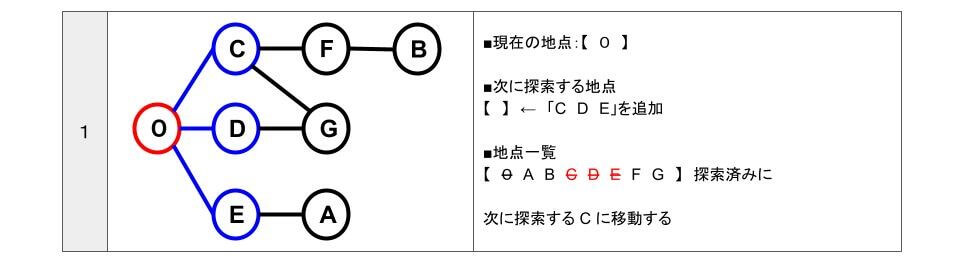
開始地点０から行ける地点は「C　D　E」です。
「C　D　E」は、すべて未探索なので「次に探索する地点」に「C　D　E」を追加します。
地点一覧から「C　D　E」を探索済みにします。
「次に探索する地点」【　C　D　E　】のうち、一番初めに追加している「C」に移動します。
C に移動したので「次に探索する地点」の「C」を削除します。

ステップ２

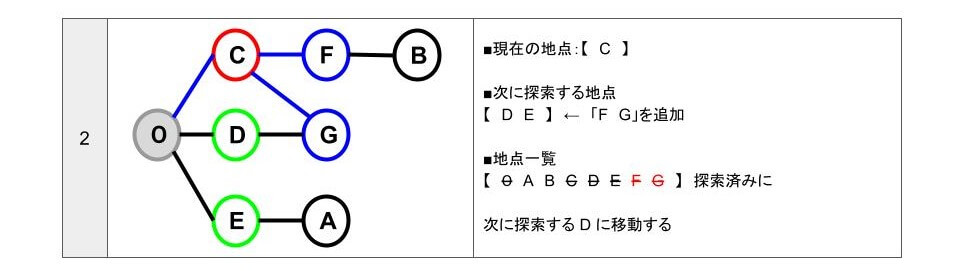
C 地点から行ける地点は「０　F　G」です。
「０　F　G」のうち、「０」は探索済み、「F　G」は未探索です。
「次に探索する地点」に、未探索の「F　G」追加します。
地点一覧から「F　G」を探索済みにします。
「次に探索する地点」【　D　E　F　G　】のうち、一番初めに追加している「D」に移動します。
D に移動したので「次に探索する地点」の「D」を削除します。

ステップ３

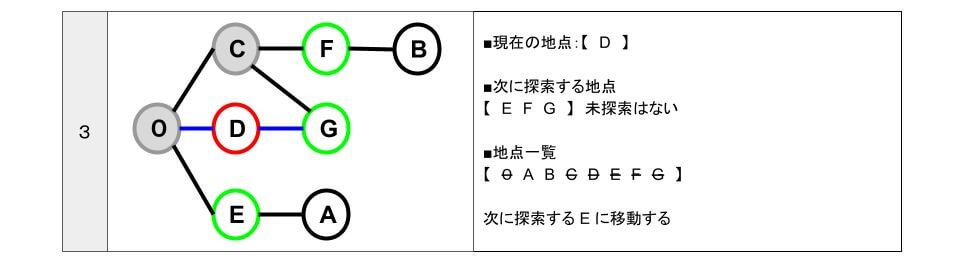
D 地点から行ける地点は「０　G」です。
「０　G」は、すべて探索済みです。
「次に探索する地点」【　E　F　G　】のうち、一番初めに追加している「E」に移動します。
E に移動したので「次に探索する地点」の「E」を削除します。

ステップ４

E 地点から行ける地点は「０　A」です。
「０　A」のうち、「０」は探索済み、「A」は未探索です。
「次に探索する地点」に、未探索の「A」追加します。
地点一覧から「A」を探索済みにします。
「次に探索する地点」【　F　G　A　】のうち、一番初めに追加している「F」に移動します。
F に移動したので「次に探索する地点」の「F」を削除します。

ステップ５

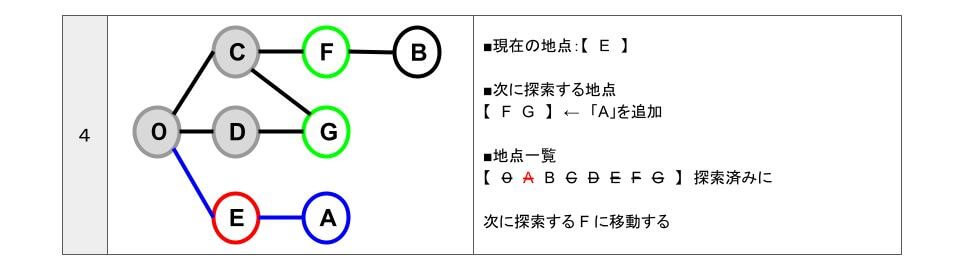
F 地点から行ける地点は「C　B」です。
「C　B」のうち、「C」は探索済み、「B」は未探索です。
「次に探索する地点」に、未探索の「B」追加します。
地点一覧から「B」を探索済みにします。
「次に探索する地点」【　G　A　B　】のうち、一番初めに追加している「G」に移動します。
G に移動したので「次に探索する地点」の「G」を削除します。

ステップ６

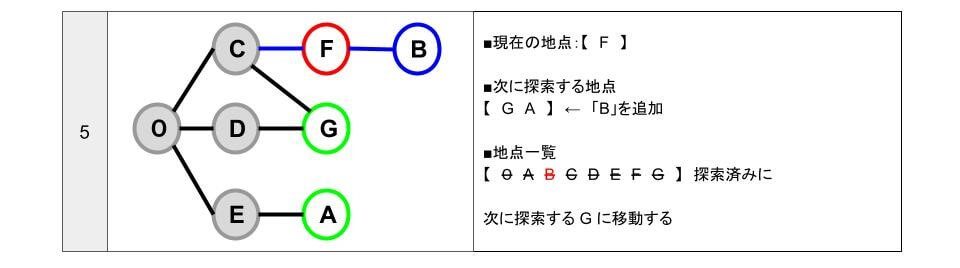
G 地点から行ける地点は「C　D」です。
「C　D」は、すべて探索済みです。
「次に探索する地点」【　A　B　】のうち、一番初めに追加している「A」に移動します。
A に移動したので「次に探索する地点」の「A」を削除します。

ステップ７

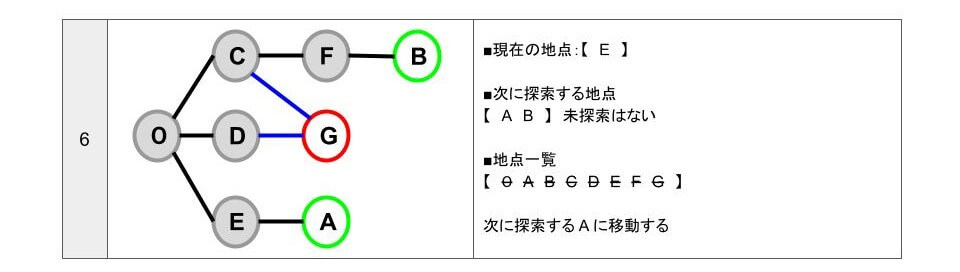
A 地点から行ける地点は「E」です。
「E」は、探索済みです。
「次に探索する地点」【　B　】のうち、一番初めに追加している「B」に移動します。
B に移動したので「次に探索する地点」の「B」を削除します。

ステップ８

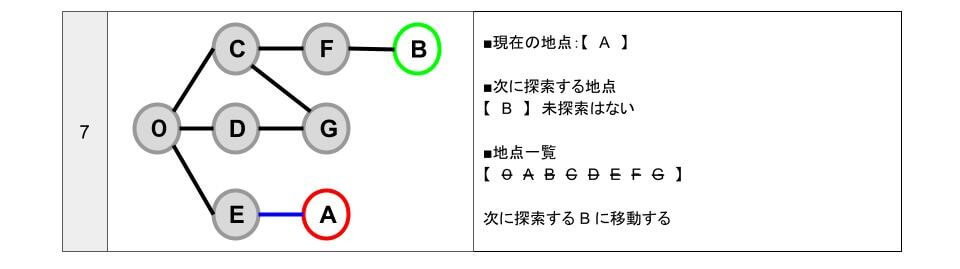
B 地点から行ける地点は「F」です。
「F」は、探索済みです。
「次に探索する地点」がなくなったので探索を終了します。

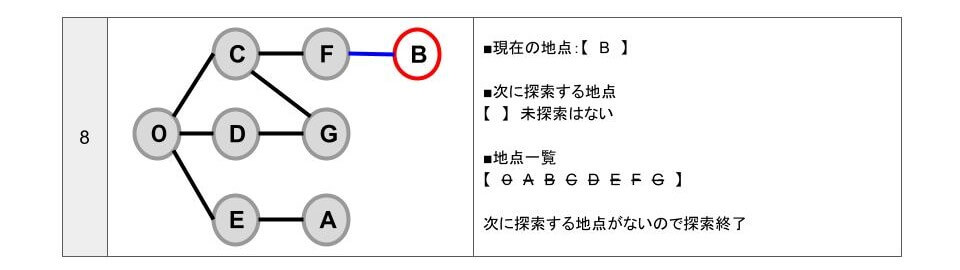
このように、探索する順番は、０→C→D→E→F→G→A→B になります。

開始地点０から

１回でたどりつけるところ：C、D、E
２回でたどりつけるところ：F、G、A
３回でたどりつけるところ：B

０→【C→D→E】→【F→G→A】→【B】というように開始地点から近い順に探索されています。

キューとの関係性

ここまで見てきたように、幅優先探索は、次のように探索を行います。

探索開始地点を、「次に探索する地点」に追加する。
探索開始地点を探索済みにする。
「次に探索する地点」に追加されている地点に移動する。
移動した地点から行ける地点のうち、未探索の地点を「次に探索する地点」に追加する。
4で「次に探索する地点」に追加した地点を探索済みにする。
「次に探索する地点」が空でなければ、「次に探索する地点」の一番初めに追加された地点に移動する
４に戻る

重要なのが「次に探索する地点」の管理です。

「次に探索する地点」には、『地点の追加』と『一番初めに追加された地点の取り出し』ということを行います。

これは、キューを使って管理することで、探索順序を制御できます。

キューは、データ構造の１つで、先入れ先出し（FIFO：First In First Out）の規則に従ってデータを管理します。

キューの基本的な操作としては次のようなものがあります。

enqueue：キューに一番後ろに要素を追加する。
dequeue：キューの一番前の要素を取り出す。

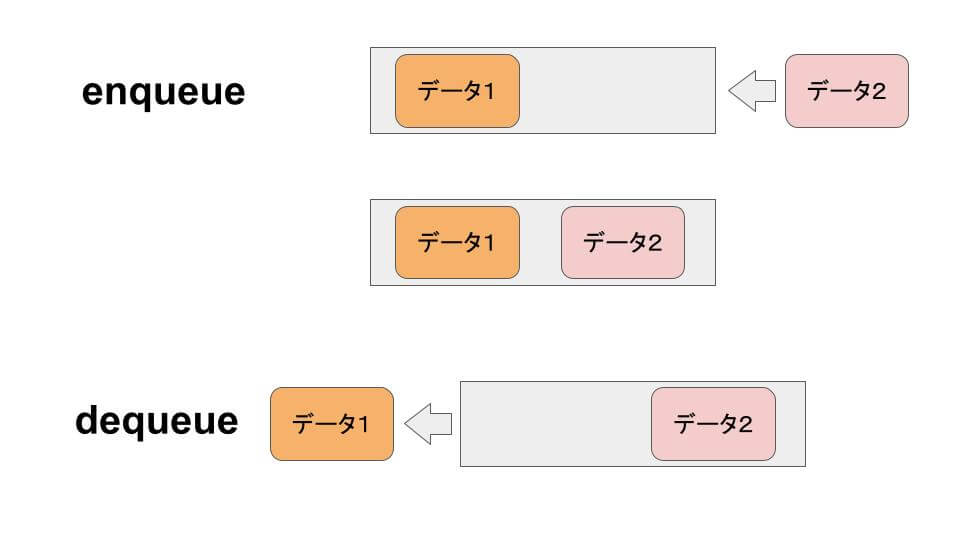
地点の追加は enqueue、一番初めに追加された地点の取り出しは dequeue を使うことで実現できます。

Pythonでは、リストをキューとして使うことができます。

末尾に要素を追加する enqueue は、append() メソッドを使い、先頭の要素を取り出す dequeue は、pop(0) メソッドを使います。

# キューをリストとして宣言
queue = []

# キューの末尾に要素を追加する
queue.append('ant')
queue.append('dog')

print(queue)		# => ['ant', 'dog']


# a にキューの先頭の要素を取り出して格納する
a = queue.pop(0)

print(a)			# => ant
print(queue)		# => ['dog']


# キューの末尾に要素を追加する
queue.append('cat')
print(queue)		# => ['dog', 'cat']

【Python】list の使い方

ただし、リストをキューとして使うとき、先頭の要素を取り出す処理に時間がかかるので注意が必要です。

そのため、計算量が多くなるときは、collections.deque を使えば、リストを使うより高速にキューを実装できます。

末尾に要素を追加する enqueue は、append() メソッドを使い、先頭の要素を取り出す dequeue は、popleft() メソッドを使います。

# collections モジュールから deque クラスをインポートする
from collections import deque

# キューを宣言
queue = deque()

# キューの末尾に要素を追加する
queue.append('ant')
queue.append('dog')

print(queue)		# => deque(['ant', 'dog'])


# a にキューの先頭の要素を取り出して格納する
a = queue.popleft()

print(a)			# => ant
print(queue)		# => deque(['dog'])


# キューの末尾に要素を追加する
queue.append('cat')
print(queue)		# => deque(['dog', 'cat'])

キューを使うことで、幅優先探索の効率的な実装が可能になります。

幅優先探索の基本コード

幅優先探索のアルゴリズムは、次のようになります。

探索開始地点をキューに追加する。
キューが空になるまで次の操作を行う。
- キューから先頭の要素を取り出す。
- 先頭の要素から行くことのできる、未探索の地点をキューに入れて探索済みにする

これを実装したコードは次のようになります。

各地点がどこにつながっているかは graph という名前のリストで管理しています。

# キューの宣言
queue = deque()
# N 個の地点すべてを未探索に
searched = [False] * N

# 探索開始地点をキューに追加する
queue.append(0)
# 探索開始地点を探索済みに
searched[0] = True

# キューが空になるまで繰り返す
while queue:
    # キューの先頭の要素を取り出す
    v = queue.popleft()

    # 取り出した地点から行ける地点について繰り返す
    for next_v in graph[v]:
        # 行ける地点が探索済みならスキップ
        if searched[next_v]:
            continue

        # 行ける地点をキューに追加する
        queue.append(next_v)
        # 行ける地点を探索済みにする
        searched[next_v] = True

この処理が終わったあとに、searched を確認することで、探索開始地点から行ける地点がわかります。

このコードについての詳しい説明は、後ほど行います。

問題を解いてみる

競技プログラミングの鉄則 ~アルゴリズム力と思考力を高める77の技術~ に掲載されている問題を幅優先探索を使って解いてみます。

この問題は AtCoder の自動採点システムで提供されています。

A62 – Depth First Search

問題へのリンク

この問題を簡単に説明すると、探索開始地点からすべての頂点に行くことができるかを判定する問題です。

この問題の解答コードが、次のコードです。

幅優先探索についてのコードは、先ほど紹介した基本コードと同じものです。

# collections モジュールから deque クラスをインポートする
from collections import deque

# 入力
N, M = map(int, input().split())

# グラフの入力
graph = [[] for _ in range(N)]
for _ in range(M):
    A, B = map(int, input().split())
    A -= 1
    B -= 1
    graph[A].append(B) 
    graph[B].append(A)
    

#  *************** 幅優先探索 ***************

# キューの宣言
queue = deque()
# N 個の頂点すべてを未探索に
searched = [False] * N

# 探索開始する頂点をキューに追加する
queue.append(0)
# 探索開始する頂点を探索済みに
searched[0] = True

# キューが空になるまで繰り返す
while queue:
    # キューの先頭の要素を取り出す
    v = queue.popleft()

    # 取り出した頂点とつながっている各頂点について処理
    for next_v in graph[v]:
        # つながっている頂点が探索済みならスキップ
        if searched[next_v]:
            continue

        # つながっている頂点をキューに追加する
        queue.append(next_v)
        # つながっている頂点を探索済みにする
        searched[next_v] = True

#  ************ 幅優先探索の終了 ************


# すべての頂点が探索済みか確認
for i in range(N):
    # 探索済みの時はスキップ
    if searched[i]:
        continue
    
    # 未探索のときは出力して終了
    print('The graph is not connected.')
    exit()

# すべての頂点が探索済み
print('The graph is connected. ')

入力の受け取り

まずは、入力の受け取りです。

2行目の「 from collections import deque 」は、幅優先探索で使うキューのために必要なコードになります。

問題文のとおり、N 頂点 M 辺を表す N と M を受け取っています。

# collections モジュールから deque クラスをインポートする
from collections import deque

# 入力
N, M = map(int, input().split())

【Python】input の使い方

辺を結ぶ A_i と B_i の受け取りですが、一般にグラフは隣接リスト表現で受け取ることが多いです。

次のように入力を受け取ります。

# 入力
N, M = map(int, input().split())

# グラフ
graph = [[] for _ in range(N)]

# 入力
for _ in range(M):
    A, B = map(int, input().split())
    
    # 隣接する頂点を追加
    graph[A].append(B)
    graph[B].append(A)	# 有向グラフの場合この行は不要

A62 – Depth First Search の入力例２で説明します。

入力例２

与えられたグラフは次のようになります。

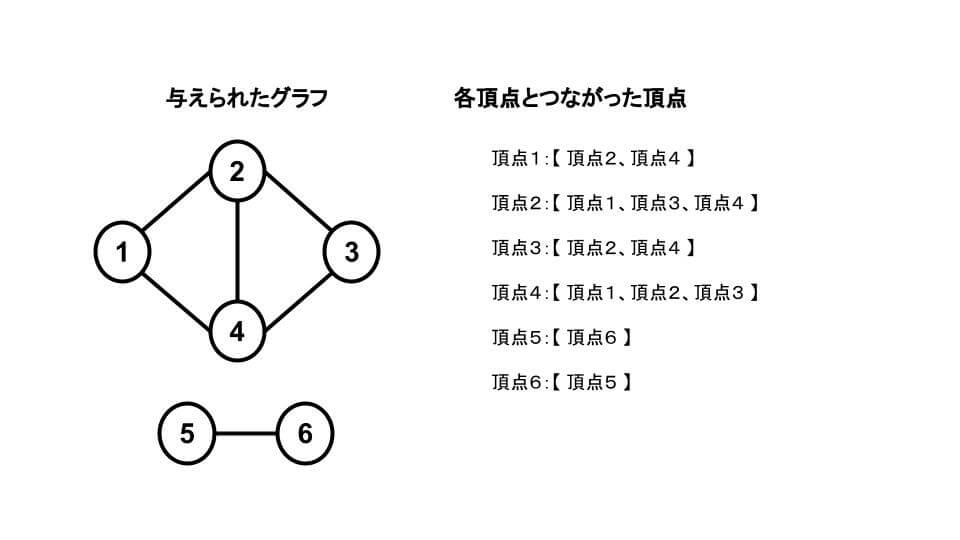
隣接リスト表現のグラフは、2次元のリスト（graph）でグラフの連結を管理します。

たとえば、頂点１とつながった【頂点２，頂点４】というのを graph[1] = [2, 4] のように管理します。

これは、頂点１は、頂点２と頂点４につながっていることを表しています。

同様に、頂点２だと、頂点１と頂点３と頂点４につながっているので graph[2] = [1, 3, 4] になります。

このように、グラフは、リストを要素に持った、要素の数が N の２次元のリストで管理できます。

どこにもつながっていない N 個の頂点は、要素の数が N の空の2次元のリストになります。

それがを作っているのが graph = [[] for _ in range(N)] です。

graph = [[] for _ in range(N)] は、リスト内包表記を利用して、空の2次元のリストを作成しています。

# N が６のとき
N = 6

# グラフ
graph = [[] for _ in range(N)]

print(graph)	# => [[], [], [], [], [], []]

【Python】list の使い方 – リスト内包表記

あとは、辺を結ぶ A_i と B_i の受け取り、グラフの連結を管理している graph に追加していきます。

頂点１と頂点４がつながっているときは、graph[1] = [4] と graph[4] = [1] のようにそれぞれに追加する必要があります。

append() メソッドを使ってリストに要素を追加していきます。

# 入力
for _ in range(M):
    A, B = map(int, input().split())
    
    # 隣接する頂点を追加
    graph[A].append(B)
    graph[B].append(A)	# 有向グラフの場合この行は不要

これから、入力を受け取るためのコードは、次のようになります。

先ほどの幅優先探索の基本コードと graph = [[] for _ in range(N)] 部分の N が N+1 に変わっていることに注意してください。

これは graph = [[] for _ in range(N)] のままだと、リストのインデックスが５までしかないためです。

この場合、存在しない頂点０が graph に存在するようになります。

# 入力
N, M = map(int, input().split())

# グラフ
graph = [[] for _ in range(N + 1)]

# 入力
for _ in range(M):
    A, B = map(int, input().split())
    
    # 隣接する頂点を追加
    graph[A].append(B)
    graph[B].append(A)

# グラフのリストの確認
print(f'グラフのリスト：{graph}')

# 各頂点の確認
for i in range(1, N + 1):
    print(f'頂点{i}：{graph[i]}')

"""出力結果
グラフのリスト：[[], [4, 2], [3, 1, 4], [2, 4], [1, 3, 2], [6], [5]]
頂点1：[4, 2]
頂点2：[3, 1, 4]
頂点3：[2, 4]
頂点4：[1, 3, 2]
頂点5：[6]
頂点6：[5]
"""

出力結果から、図で見たときの「各頂点とつながった頂点」と一致していることが確認できます。

グラフを graph = [[] for _ in range(N)] で使いたい場合は、次のようになります。

辺を結ぶ A_i と B_i の受け取りのときに、各頂点番号を１引いてグラフに追加していきます。

こうすることで、要素の数が N のグラフで管理することができます。

出力結果の各頂点は実際の頂点番号の１引いた数になっています。

# 入力
N, M = map(int, input().split())

# グラフ
graph = [[] for _ in range(N)]

# 入力
for _ in range(M):
    A, B = map(int, input().split())
    # リストで管理しやすいように -1
    A -= 1
    B -= 1
    
    # 隣接する頂点を追加
    graph[A].append(B)
    graph[B].append(A)

# グラフのリストの確認
print(f'グラフのリスト：{graph}')

"""出力結果
グラフのリスト：[[3, 1], [2, 0, 3], [1, 3], [0, 2, 1], [5], [4]]
"""

今回の問題ではこちらのコードを使って解説していきます。

各頂点を探索する

入力が受け取れたので、グラフ全体が連結であるかを判定します。

グラフ全体が連結の場合は、いずれかの頂点から幅優先探索すれば、すべての頂点が探索済みになります。

もし、未探索の頂点があれば、そのグラフはグラフ全体が連結ではありません。

幅優先探索をするコードが次のコードです。

探索する順番についてわかりやすくするために、適宜出力するようにしています。

# collections モジュールから deque クラスをインポートする
from collections import deque

# 入力
N, M = map(int, input().split())

# グラフの入力
graph = [[] for _ in range(N)]
for _ in range(M):
    A, B = map(int, input().split())
    A -= 1
    B -= 1
    graph[A].append(B) 
    graph[B].append(A)
    
print('幅優先探索開始')
    
#  *************** 幅優先探索 ***************

# キューの宣言
queue = deque()
# N 個の頂点すべてを未探索に
searched = [False] * N

# 探索開始する頂点をキューに追加する
queue.append(0)
# 探索開始する頂点を探索済みに
searched[0] = True

# キューが空になるまで繰り返す
while queue:
    print(f'キュー：{queue}')
    print(f'探索済み：{searched}')
    # キューの先頭の要素を取り出す
    v = queue.popleft()
    print(f'頂点{v+1}を探索する')
    
    # 取り出した頂点とつながっている各頂点について処理
    for next_v in graph[v]:
        print(f'頂点{v+1}とつながっている頂点{next_v+1}を確認')
        # つながっている頂点が探索済みならスキップ
        if searched[next_v]:
            print(f'頂点{next_v+1}は探索済みのためスキップ')
            print()
            continue

        print(f'頂点{next_v+1}は未探索のためキューに追加して、探索済みにする')
        # つながっている頂点をキューに追加する
        queue.append(next_v)
        # つながっている頂点を探索済みにする
        searched[next_v] = True
        print()

#  ************ 幅優先探索の終了 ************

print('幅優先探索終了')

これを実行した結果は次のようになります。

キューと探索済みのリストの数字は、頂点の番号から１引いたものになっています。

幅優先探索開始
キュー：deque([0])
探索済み：[True, False, False, False, False, False]
頂点1を探索する
頂点1とつながっている頂点4を確認
頂点4は未探索のためキューに追加して、探索済みにする

頂点1とつながっている頂点2を確認
頂点2は未探索のためキューに追加して、探索済みにする

キュー：deque([3, 1])
探索済み：[True, True, False, True, False, False]
頂点4を探索する
頂点4とつながっている頂点1を確認
頂点1は探索済みのためスキップ

頂点4とつながっている頂点3を確認
頂点3は未探索のためキューに追加して、探索済みにする

頂点4とつながっている頂点2を確認
頂点2は探索済みのためスキップ

キュー：deque([1, 2])
探索済み：[True, True, True, True, False, False]
頂点2を探索する
頂点2とつながっている頂点3を確認
頂点3は探索済みのためスキップ

頂点2とつながっている頂点1を確認
頂点1は探索済みのためスキップ

頂点2とつながっている頂点4を確認
頂点4は探索済みのためスキップ

キュー：deque([2])
探索済み：[True, True, True, True, False, False]
頂点3を探索する
頂点3とつながっている頂点2を確認
頂点2は探索済みのためスキップ

頂点3とつながっている頂点4を確認
頂点4は探索済みのためスキップ

幅優先探索終了
キュー：deque([])
探索済み：[True, True, True, True, False, False]

頂点１から幅優先探索をした結果、頂点５と頂点６は未探索になっています。

すべての頂点が探索済みか確認する

探索終了後、searched のすべての値が True であれば、すべての頂点が探索済み（＝グラフ全体が連結している）ということになります。

searched の各値を True か判定して、答えを出力しているのが次のコードです。

for 文の中で、searched のいずれかの値が False だったときは、答えを出力して処理を終了しています。

# すべての頂点が探索済みか確認
for i in range(N):
    # 探索済みの時はスキップ
    if searched[i]:
        continue
    
    # 未探索のときは出力して終了
    print('The graph is not connected.')
    exit()

# すべての頂点が探索済み
print('The graph is connected. ')

解答コード

次のコードがこの問題の解答コード（再掲）になります。

# collections モジュールから deque クラスをインポートする
from collections import deque

# 入力
N, M = map(int, input().split())

# グラフの入力
graph = [[] for _ in range(N)]
for _ in range(M):
    A, B = map(int, input().split())
    A -= 1
    B -= 1
    graph[A].append(B) 
    graph[B].append(A)
    

#  *************** 幅優先探索 ***************

# キューの宣言
queue = deque()
# N 個の頂点すべてを未探索に
searched = [False] * N

# 探索開始する頂点をキューに追加する
queue.append(0)
# 探索開始する頂点を探索済みに
searched[0] = True

# キューが空になるまで繰り返す
while queue:
    # キューの先頭の要素を取り出す
    v = queue.popleft()

    # 取り出した頂点とつながっている各頂点について処理
    for next_v in graph[v]:
        # つながっている頂点が探索済みならスキップ
        if searched[next_v]:
            continue

        # つながっている頂点をキューに追加する
        queue.append(next_v)
        # つながっている頂点を探索済みにする
        searched[next_v] = True

#  ************ 幅優先探索の終了 ************


# すべての頂点が探索済みか確認
for i in range(N):
    # 探索済みの時はスキップ
    if searched[i]:
        continue
    
    # 未探索のときは出力して終了
    print('The graph is not connected.')
    exit()

# すべての頂点が探索済み
print('The graph is connected. ')

幅優先探索を使って解く問題について、実装方法について解説した記事もあるのでぜひ読んでみてください。

【Python】幅優先探索のいろいろな実装方法