【AtCoder】ABC245 – C問題について解説【Python】

abc245-c プログラミング

そまちょブログのそまちょ（@somachob）です。

この記事は、AtCoder Beginner Contest 245 の C問題についての解説です。

C – Choose Elements

問題へのリンク

入力例１をもとに、解説します。

入力例１
5 4
9 8 3 7 2
1 6 2 9 5

まずは、入力を受け取ります。

【Python】input の使い方
プログラムでは、入力を受け取って処理することは多いです。 Python での入力は input() を使います。 この記事では input() について解説します。 Python の出力については、こちらの記事で解説しています。 入力を受け...
somachob.com
2023.03.03
 
# 入力
N, K = map(int, input().split())
A = list(map(int, input().split()))
B = list(map(int, input().split()))

# 入力の確認用
print(N,K)
print(A)
print(B)

"""出力結果
5 4
[9, 8, 3, 7, 2]
[1, 6, 2, 9, 5]
"""

A と B の数列は、リストで管理しています。

全探索できるか

条件は次の２つです。

  1. すべての i （1 ≦ i ≦ N）について、Xi = Ai または Xi=Bi
  2. すべての i （1 ≦ i ≦ N – 1）について、| Xi – Xi+1 | ≦ K

条件１を満たす数列 X をすべて列挙して、その列挙したすべての数列 X について、条件２を満たすか確認することで解答することができます。

たとえば、次のような再帰関数を使ったコードですべての数列 X を列挙することができます。

ほかにもビット全探索を使う方法もあります。

# 入力
N, K = map(int, input().split())
A = list(map(int, input().split()))
B = list(map(int, input().split()))

# 再帰関数で全列挙
def rec(i, X):
    # ベースケース
    if len(X) == N:
        print(X)
        return
  
    # A を選択
    X.append(A[i])
    rec(i+1, X)
    X.pop()
  
    # B を選択
    X.append(B[i])
    rec(i+1, X)
    X.pop()


rec(0, [])


"""実行結果
[9, 8, 3, 7, 2]
[9, 8, 3, 7, 5]
[9, 8, 3, 9, 2]
[9, 8, 3, 9, 5]
[9, 8, 2, 7, 2]
[9, 8, 2, 7, 5]
[9, 8, 2, 9, 2]
[9, 8, 2, 9, 5]
[9, 6, 3, 7, 2]
[9, 6, 3, 7, 5]
[9, 6, 3, 9, 2]
[9, 6, 3, 9, 5]
[9, 6, 2, 7, 2]
[9, 6, 2, 7, 5]
[9, 6, 2, 9, 2]
[9, 6, 2, 9, 5]
[1, 8, 3, 7, 2]
[1, 8, 3, 7, 5]
[1, 8, 3, 9, 2]
[1, 8, 3, 9, 5]
[1, 8, 2, 7, 2]
[1, 8, 2, 7, 5]
[1, 8, 2, 9, 2]
[1, 8, 2, 9, 5]
[1, 6, 3, 7, 2]
[1, 6, 3, 7, 5]
[1, 6, 3, 9, 2]
[1, 6, 3, 9, 5]
[1, 6, 2, 7, 2]
[1, 6, 2, 7, 5]
[1, 6, 2, 9, 2]
[1, 6, 2, 9, 5]
"""

あとは、列挙した数列について、条件２を満たすか判定します。

# 入力
N, K = map(int, input().split())
A = list(map(int, input().split()))
B = list(map(int, input().split()))


# 数列 X が条件２を満たすか判定
def check(X):
    for i in range(N-1):
        # 条件２を満たさない
        if abs(X[i] - X[i+1]) > K:
            return
    
    # 条件２を満たす
    print('Yes')
    exit()


# 再帰関数で全列挙
def rec(i, X):
    # ベースケース
    if len(X) == N:
        check(X)	# 条件２を満たすか判定
        return
  
    # A を選択
    X.append(A[i])
    rec(i+1, X)
    X.pop()
  
    # B を選択
    X.append(B[i])
    rec(i+1, X)
    X.pop()

    
# 再帰関数で全探索
rec(0, [])

# 条件を満たす X が存在しない
print('No')

しかし、条件１を満たす数列 X の数は、長さ N が大きくなるにつれて多くなります。

長さ N が１だと２通り（２＝２１）。

長さ N が２だと４通り（２×２＝２２）。

長さ N が３だと８通り（２×２×２＝２３）。

長さ N が４だと１６通り（２×２×２×２＝２４）。

長さ N が N だと２N通り。

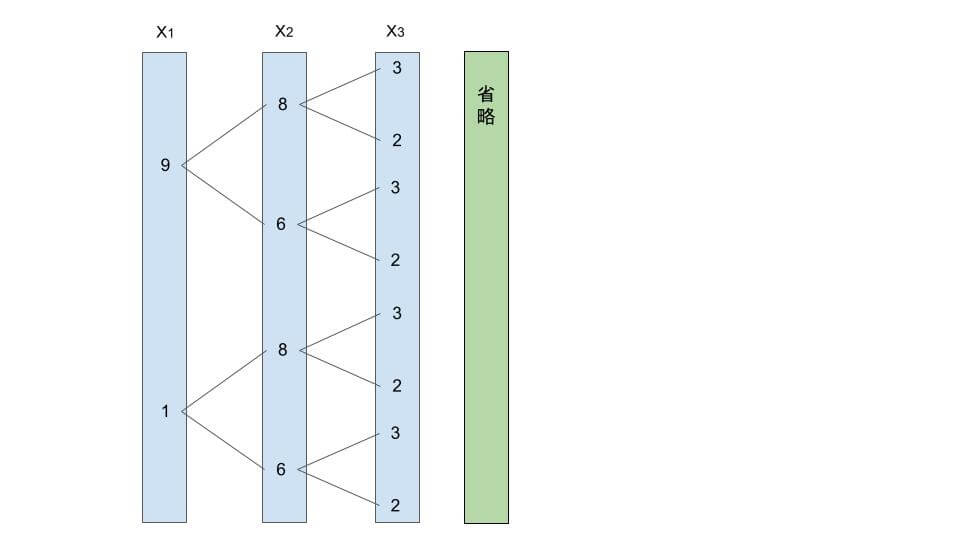
abc245-rec2

問題文の制約から N は ２×１０５なので、全探索は間に合いません。

別の方法で解く

２つの条件を満たす長さ N の数列 X について考えます。

i = 1 のときについて考えると、A =（9, 8, 3, 7, 2）、B = (1, 6, 2, 9, 5）なので

条件１から、X1 は A1 = 9 または B1 = 1 のどちらかです。

条件２のうち、Xi+1 は i = 1 なので Xi+1 は X2 になります。つまり、X2 は、A2 = 8 または B2 = 6 のどちらかになります。

X1 を 9 だとすれば、| 9 – 8 | = 1 または | 9 – 6 | = 3

X1 を 1 だとすれば、| 1 – 8 | = 7 または | 1 – 6 | = 5

K は ４なので、条件を満たすのは X1 = 9 です。

このように考えていくことで、条件を満たす数列 X が存在するか確認することができます。

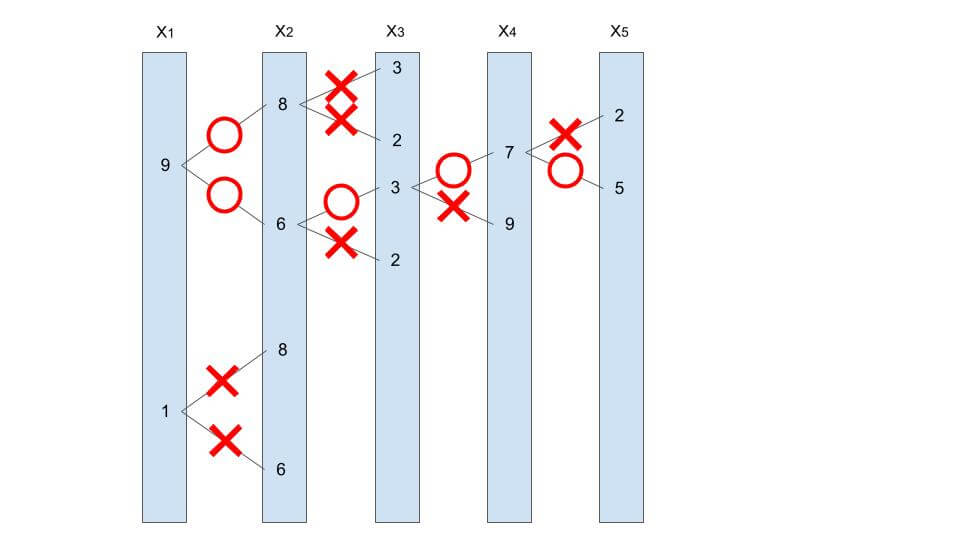
abc245-rec

最終的に i が N – 1 まで条件を満たすか確認できれば数列 X が存在し、そうでないときは数列 X は存在しないということになります。

再帰関数で、次のように書きます。

# 入力
N, K = map(int, input().split())
A = list(map(int, input().split()))
B = list(map(int, input().split()))


# 再帰関数で探索
def rec(i, X):
    if i == N-1:
        return True
  
    # 処理



if rec(0, A[0]) or rec(0, B[0]):
    print('Yes')
else:
    print('No')

先ほどのコードに処理などの肉付けをしたのが次のコードです。

# 入力
N, K = map(int, input().split())
A = list(map(int, input().split()))
B = list(map(int, input().split()))


# 再帰関数で探索
def rec(i, X):
    if i == N-1:
        return True
  
    # A[i+1] が条件２を満たすとき
    if abs(X - A[i+1]) <= K:
      if rec(i+1, A[i+1]):
        return True
  
    # B[i+1] が条件２を満たすとき
    if abs(X - B[i+1]) <= K:
      if rec(i+1, B[i+1]):
        return True

    # A[i+1] も B[i+1] もダメなとき
    return False
    

if rec(0, A[0]) or rec(0, B[0]):
    print('Yes')
else:
    print('No')

これでもまだ、ACできません。

再帰回数のスタックオーバーフロー

再帰関数の呼び出し回数が多くなれば、スタックオーバーフローが発生する可能性があり、スタックのサイズに一定の制限が設けられています。

再帰関数のスタックの制限を変更するために、次のコードを追加します。

import sys
sys.setrecursionlimit(10**6)

追加したコードが次です。

# 再帰関数のスタック数を変更
import sys
sys.setrecursionlimit(10**6)


# 入力
N, K = map(int, input().split())
A = list(map(int, input().split()))
B = list(map(int, input().split()))


# 再帰関数で探索
def rec(i, X):
    if i == N-1:
        return True
  
    # A[i+1] が条件２を満たすとき
    if abs(X - A[i+1]) <= K:
      if rec(i+1, A[i+1]):
        return True
  
    # B[i+1] が条件２を満たすとき
    if abs(X - B[i+1]) <= K:
      if rec(i+1, B[i+1]):
        return True

    # A[i+1]もB[i+1]もダメなとき
    return False
    

if rec(0, A[0]) or rec(0, B[0]):
    print('Yes')
else:
    print('No')

実はこれでも、ACはできません。

何度も同じ引数の再帰関数を実行してしまうためです。

それを改善するのがメモ化再帰です。

メモ化再帰

Pythonでは、lru_cache という機能を使えばメモ化再帰を簡単に書くことができます。

ライブラリをインポートして、@lru_cache というデコレータを関数の頭につけます。

# 再帰関数のスタック数を変更
import sys
sys.setrecursionlimit(10**6)

#メモ化再帰
from functools import lru_cache


# 入力
N, K = map(int, input().split())
A = list(map(int, input().split()))
B = list(map(int, input().split()))


# 再帰関数で探索
@lru_cache(maxsize=None)
def rec(i, X):
    if i == N-1:
        return True
  
    # A[i+1] が条件２を満たすとき
    if abs(X - A[i+1]) <= K:
      if rec(i+1, A[i+1]):
        return True
  
    # B[i+1] が条件２を満たすとき
    if abs(X - B[i+1]) <= K:
      if rec(i+1, B[i+1]):
        return True

    # A[i+1]もB[i+1]もダメなとき
    return False
    

if rec(0, A[0]) or rec(0, B[0]):
    print('Yes')
else:
    print('No')

これでACできました。

再帰関数のときは、PyPy より Python の方が実行速度が速いようなので、提出する際の言語に注意してください。

PyPyで提出したとき、１件のテストケースでTLEしました。

参考

タイトルとURLをコピーしました