そまちょブログのそまちょ(@somachob)です。
競技プログラミングにおいて、再帰関数は非常に重要なテクニックの1つです。
初心者にとって、再帰関数は理解するのが難しいと感じることも多いです。
この記事では、超初心者でもわかるように再帰関数の基礎について、Pythonのコード例を交えて解説していきます。
再帰関数について初めて学ぶ方も、再帰関数を使ったアルゴリズムを理解したい方も、ぜひ参考にしてください。
再帰関数とは
再帰関数とは、自分自身を呼び出す関数のことです。
再帰関数は、問題を小さな部分問題に分割して、それを再帰的に解くことで全体の問題を解決する方法です。
再帰関数の基本的な考え方
再帰関数を理解するためには、再帰的な処理の基本的な考え方を理解することが重要です。
再帰関数の基本的な考え方は、次のようになります。
- 問題を小さな問題に分割する。
- 分割した問題を自分自身に渡す。
- 1と2を再帰的に繰り返して、最終的な答えを求める。
たとえば、階乗を計算するコードについて考えてみます。階乗は、1からある数までの連続する整数の積のことです。
1からnまでの階乗を表す n! は、n*(n-1)*(n-2)・・・*2*1 になります。
5! を計算すれば、5*4*3*2*1 = 120 です。ちなみに、0! は 1 です。
階乗の計算を再帰関数で実装すれば、次のようになります。
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n-1)この関数は、引数 n の階乗を計算します。処理の中で自分自身を呼びだすことで、n の値が0になるまで再帰的に計算を行い、最終的に n! を求めています。
n が 3 のときの動きを順番に説明すれば次のようになります。
- factorial(3) が呼び出される。
- if 3 == 0: は false なので、else に移る。
- return 3 * factorial(2) が実行される。
- factorial(2) が呼び出される。
- if 2 == 0: は false なので、else に移る。
- return 2 * factorial(1) が実行される。
- factorial(1) が呼び出される。
- if 1 == 0: は false なので、else に移る。
- return 1 * factorial(0) が実行される。
- factorial(0) が呼び出される。
- if 0 == 0: は true なので、return 1が実行される。
- factorial(0) は 1 が返されるので return 1 * factorial(0) は、return 1 * 1になる。
- factorial(1) は 1 が返されるので return 2 * factorial(1) は、return 2 * 1になる。
- factorial(2) は 2 が返されるので return 3 * factorial(2) は、return 3 * 2になる。
- factorial(3) は 6 が返される。
処理の流れを出力をするために、先ほどのコードを少し変更して実行した結果です。
def factorial(n):
print(f'factorial({n})が呼び出されました。')
if n == 0:
print(f'{n} == 0 は True です。')
print(f'factorial({n})は 1 を返します。')
return 1
else:
print(f'{n} == 0 は False です。')
ret = factorial(n-1)
print(f'{n} * factorial({n-1}) は {n} * {ret} です。')
print(f'factorial({n}) は {n * ret} を返します。')
return n * ret
print(factorial(3)) # => 6
"""実行結果
factorial(3)が呼び出されました。
3 == 0 は False です。
factorial(2)が呼び出されました。
2 == 0 は False です。
factorial(1)が呼び出されました。
1 == 0 は False です。
factorial(0)が呼び出されました。
0 == 0 は True です。
factorial(0)は 1 を返します。
1 * factorial(0) は 1 * 1 です。
factorial(1) は 1 を返します。
2 * factorial(1) は 2 * 1 です。
factorial(2) は 2 を返します。
3 * factorial(2) は 3 * 2 です。
factorial(3) は 6 を返します。
6
"""この例からわかるように、再帰関数は問題を小さく分割していくことで、最終的な解答を得るトップダウン的な処理になります。
5の階乗を計算するときは、次のように使います。
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n-1)
print(factorial(5)) # => 120再帰関数の実装
再帰関数は、自分自身を呼び出すことによって、処理を繰り返します。つまり、同じ関数を繰り返し呼び出して処理を行います。
しかし、再帰を終了する条件がないと、処理が無限に繰り返されてしまいます。
そのため、再帰関数には「ベースケース」という、再帰を終了する条件が必要です。
再帰関数は、次のような流れで処理が進みます。
- 再帰関数が呼び出される。
- ベースケースかどうか判定する。
- ベースケースなら、処理を終了し、値を返す。
- ベースケースでなければ、再帰ステップで自分自身を呼び出す。
- 1から4を繰り返し、ベースケースに到達するまで処理を繰り返す。
ベースケースと再帰ステップ
再帰関数は、ベースケースと再帰ステップから構成されます。
- ベースケース:再帰を終了するための条件。
- 再帰ステップ:問題をより小さい問題に分割し、自分自身を呼び出す部分。
基本的な構造は次のようになります。
def 関数名(引数):
# ベースケース
if 条件:
return 値
# 再帰ステップ
else:
return 関数名(引数を更新した値)たとえば、階乗を計算する再帰関数では、次の部分がベースケースと再帰ステップになります。
def factorial(n):
if n == 0: # ベースケース
return 1
else: # 再帰ステップ
return n * factorial(n-1)再帰関数の例題
再帰関数の例題として、ユークリッドの互除法、二分探索、フィボナッチ数列について紹介します。
ユークリッドの互除法
最大公約数は、2つの整数が共通に持つ約数のうち最大のものです。
たとえば、24 と 18 の最大公約数は 6 です。
ユークリッドの互除法は、2つの整数の最大公約数を求めるアルゴリズムです。
2つの整数が a, b のとき、a を b で割った余りを r とすれば、a と b の最大公約数は、 b と r の最大公約数に等しいという性質があります。
a を b で割った余りを r とすれば、次が成り立つ
(a と b の最大公約数)=(b と r の最大公約数)
ユークリッド互除法を再帰関数で実装したコードは次のようになります。
def gcd(a, b):
if b == 0: # ベースケース
return a
else: # 再帰ステップ
return gcd(b, a % b)この再帰関数は、b が0になるまで、再帰的に自分自身を呼び出します。b が0になれば a が最大公約数になるので a を返します。
二分探索
二分探索は、昇順または降順に並べられたデータの中から、目的の値を効率的に探すためのアルゴリズムです。
具体的には、次のような流れになります。
- 並び替えられたデータの真ん中の値を選択する。
- 「選択した値」と「目的の値」を比較する。
- 目的の値が小さいとき、データの左半分を対象に再帰的に探索する。
- 目的の値が大きいとき、データの右半分を対象に再帰的に探索する。
- 目的の値と等しいとき、探索を終了する。
- 目的の値が見つからないときは探索を終了する。
Pythonで実装したコードです。
def binary_search(arr, left, right, target):
# ベースケース
# 値が存在しない場合は -1 を返す
if right < left:
return -1
# 中央のインデックスを計算する
mid = (left + right) // 2
# 中央の要素が探している値と等しい場合は、そのインデックスを返す
if arr[mid] == target:
return mid
# 再帰ステップ
# 中央の要素よりも小さい場合、左側の配列を再帰的に探索する
elif arr[mid] > target:
return binary_search(arr, left, mid - 1, target)
# 中央の要素よりも大きい場合、右側の配列を再帰的に探索する
else:
return binary_search(arr, mid + 1, right, target)
この関数では、探索範囲がなくなったときか目的の値が見つかったときに処理を終了します。
再帰ステップでは、探索範囲を右半分または左半分のように分割しながら再帰的に処理を行います。
フィボナッチ数列
フィボナッチ数列は、前の2つの数の和が、次の数になる数列のことです。
次の数列がフィボナッチ数列になります。
0, 1, 1, 2, 3, 5, 8, 13, 21, ・・・
フィボナッチ数列の n 番目の数を再帰関数で求めるコードです。
def fibonacci(n):
if n == 0: # ベースケース
return 0
elif n == 1: # ベースケース
return 1
else: # 再帰ステップ
return fibonacci(n-1) + fibonacci(n-2)この再帰関数は、ベースケースとして「n が 0 または 1 のとき、0 あるいは 1 を返す」という条件を設定し、再帰ステップで、n-1 と n-2 を引数として自分自身を呼び出しています。
この方法では、n が大きくなれば計算量が急激に増えるため、実際にはメモ化などの工夫をして実装する必要があります。
再帰関数の応用
再帰関数は、競技プログラミングで幅広く使用されています。
応用例として、メモ化と探索アルゴリズムについて紹介します。
メモ化
これまで述べたように、再帰関数は、問題を小さな部分問題に分割して、それを再帰的に解くことで全体の問題を解決する方法です。
しかし、再帰関数が深くなると、同じ引数で再帰呼び出しが何度も行われることがあります。そのため、計算量が膨大になり効率が悪くなります。
この問題を解決する方法の1つが「メモ化」です。
メモ化とは、1度計算した結果を保存しておくことで、同じ計算が再度発生したときに、再び計算するのではなく、保存されている計算結果を再利用することで、効率的に処理する手法です。
再帰関数においては、再帰的に呼び出される関数の結果を、配列に保存しておけば、同じ引数に対しては再度計算する必要がありません。
先ほど紹介したフィボナッチ数列の再帰関数では、同じ引数に対する計算が何度も行われています。
次は、fibonacci(5) を実行したときの再帰関数の呼び出し状況です。同じ引数に対する計算が何度も行われていることがわかります。
def fibonacci(n):
print(f'fibonacci({n})が呼び出されました')
if n == 0: # ベースケース
return 0
elif n == 1: # ベースケース
return 1
else: # 再帰ステップ
return fibonacci(n-1) + fibonacci(n-2)
n = 5
result = fibonacci(n)
print(f'fibonacci({n})の結果:{result}')
"""実行結果
fibonacci(5)が呼び出されました
fibonacci(4)が呼び出されました
fibonacci(3)が呼び出されました
fibonacci(2)が呼び出されました
fibonacci(1)が呼び出されました
fibonacci(0)が呼び出されました
fibonacci(1)が呼び出されました
fibonacci(2)が呼び出されました
fibonacci(1)が呼び出されました
fibonacci(0)が呼び出されました
fibonacci(3)が呼び出されました
fibonacci(2)が呼び出されました
fibonacci(1)が呼び出されました
fibonacci(0)が呼び出されました
fibonacci(1)が呼び出されました
fibonacci(5)の結果:5
"""これを、メモ化することで効率化します。
次のコードでは、メモ化用の配列 memo を用意し、再帰的に呼び出しが行われる前に、memo に保存されているか確認することで効率的に計算しています。
def fibonacci(n, memo):
print(f'fibonacci({n})が呼び出されました')
# メモがあればメモを返す
if memo[n] is not None:
return memo[n]
if n == 0: # ベースケース
return 0
elif n == 1: # ベースケース
return 1
# 再帰ステップ
memo[n] = fibonacci(n-1, memo) + fibonacci(n-2, memo)
return memo[n]
n = 5
memo = [None] * (n + 1)
result = fibonacci(n, memo)
print(f'fibonacci({n})の結果:{result}')
"""実行結果
fibonacci(5)が呼び出されました
fibonacci(4)が呼び出されました
fibonacci(3)が呼び出されました
fibonacci(2)が呼び出されました
fibonacci(1)が呼び出されました
fibonacci(0)が呼び出されました
fibonacci(1)が呼び出されました
fibonacci(2)が呼び出されました
fibonacci(3)が呼び出されました
fibonacci(5)の結果:5
"""探索アルゴリズム
再帰関数を使った探索アルゴリズムとして、ここでは深さ優先探索(DFS)を紹介します。
深さ優先探索(DFS)
深さ優先探索(DFS)は、スタート地点から出発して、可能な限り深く探索していくアルゴリズムです。
具体的には、スタート地点から最初につながっている頂点を選んで、その頂点から再帰的に探索していきます。
もし行き止まりになった場合は、直前の頂点に戻り、そこから探索を続けます。このようにして、全ての頂点を探索します。
- スタート地点を訪問済みにする。
- スタート地点の隣接地点を再帰的に訪問する。
- 訪問済みの隣接地点はスキップする。
def dfs(pos, visited, graph):
# 現在の頂点を訪問済みにする
visited[pos] = True
# 今いる地点の隣接地点を順番にチェックする
for next_pos in graph[pos]:
# 未訪問の隣接地点がある場合は、その地点に移動して再帰的に探索する
if visited[next_pos] == False:
dfs(next_pos, visited, graph)この実装コードでは、pos は現在の地点、visited はこれまでに訪問した地点、graph はグラフの隣接リストです。
たとえば、以下のようなグラフがあるとします。
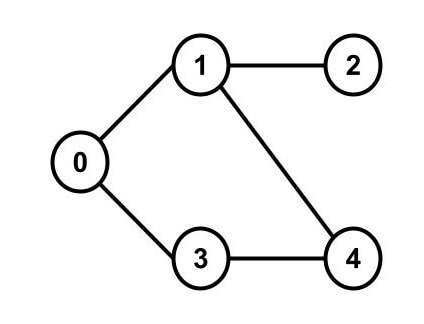
このグラフを表すと、次のようになります。
graph = {
0: [1, 3],
1: [0, 2, 4],
2: [1],
3: [0, 4],
4: [1, 3]
}このグラフで、地点0から深さ優先探索をするコードです。
def dfs(pos, visited, graph):
# 現在の頂点を訪問済みにする
visited[pos] = True
# 今いる地点の情報を表示する(任意)
print(f"Visited Node: {node}")
# 今いる地点の隣接地点を順番にチェックする
for next_pos in graph[pos]:
# 未訪問の隣接地点がある場合は、その地点に移動して再帰的に探索する
if visited[next_pos] == False:
dfs(next_pos, visited, graph)
graph = {
0: [1, 3],
1: [0, 2, 4],
2: [1],
3: [0, 4],
4: [1, 3]
}
visited = [False] * len(graph) # 訪問済みノードを管理するリスト
dfs(0, visited, graph) # ノード0からDFSを開始この実装では、各地点を訪問すると、visited にそのインデックスに対応する要素を True に設定します(訪問済みにする)。
visited は、各地点が訪問済みかどうかを記録するために使用されます。
再帰回数のスタックオーバーフロー
再帰関数を用いた深さ優先探索を紹介しました。
再帰関数の呼び出し回数が多くなれば、スタックオーバーフローが発生する可能性があります。スタックオーバーフローが発生すると、プログラムがクラッシュしたり、異常終了したりすることがあります。
グラフが大きいときや再帰が多くなる時は注意が必要です。
再帰関数を使用するときには、スタックのサイズに一定の制限が設けられています。Python では、sys.getrecursionlimit() で確認することができます。
デフォルトでは 1000 になります。これは通常の再帰関数では十分です。
import sys
print(sys.getrecursionlimit()) # => 1000競技プログラミングにおいては、1000 では不十分な時があります。
sys.setrecursionlimit(limit) を使えば、再帰の回数を増やせます。
import sys
sys.setrecursionlimit(10**6)
print(sys.getrecursionlimit()) # => 1_000_000まとめ
この記事では、再帰関数とその基本的な考え方について解説しました。
再帰関数の構造やフロー、再帰関数におけるベースケースと再帰ステップの理解を深め、基本的な再帰関数の例題であるユークリッド互除法の再帰関数やフィボナッチ数列を求める再帰関数を紹介しました。
また、再帰関数の応用として、メモ化による再帰関数の高速化や、再帰関数を用いた探索アルゴリズムである深さ優先探索(DFS)と幅優先探索(BFS)についても触れました。
再帰関数は、初心者にとっては理解しづらい概念かもしれませんが、一度理解してしまえば、プログラミングの世界で非常に強力な武器となります。ぜひ、この記事を参考に、再帰関数の基本的な考え方を理解して、再帰関数を使いこなしてください。


