【AtCoder】ABC308 – D問題について解説【Python】

そまちょブログのそまちょ（@somachob）です。

この記事は、AtCoder Beginner Contest 308 の D問題についての解説です。

D – Snuke Maze
幅優先探索
深さ優先探索
1. スタック
2. 再帰関数
参考

D – Snuke Maze

入力例１をもとに解説します。

入力例１

2 3
sns
euk

入力を受け取ります。

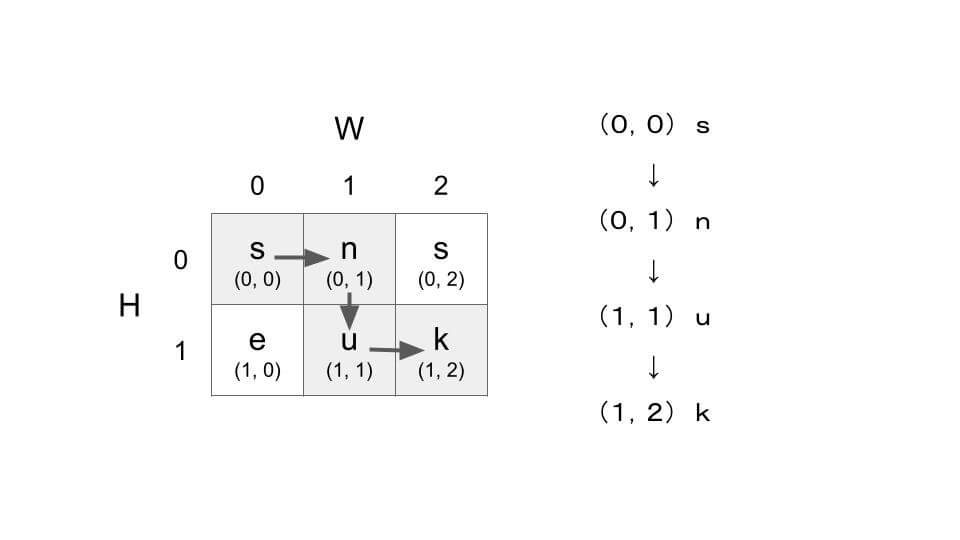
H行W列のグリッドを表す S は、（０，０）が左上を表し、右下は（H – 1、W – 1）になることに注意してください。

# 入力
H, W = map(int, input().split())
S = [input() for _ in range(H)]

# 入力確認用
print(S)
print(f'(0, 0) : {S[0][0]}')
print(f'(H-1, W-1) : {S[H-1][W-1]}')

"""出力結果
['sns', 'euk']
(0, 0) : s
(H-1, W-1) : k
"""

【Python】input の使い方

２次元で表すと次のようになり、左上（０，０）からスタートして右下（１，２）＝（H – 1、W – 1）までに s → n → u → k → e → s → n → … となるような経路が存在するか判定します。

幅優先探索

幅優先探索で解いてみます。

幅優先探索は、キューを使って探索する方法です。

実装したコードは、次のようになります。

# 入力
H, W = map(int, input().split())
S = [input() for _ in range(H)]

# 左上が s でないときは No
if S[0][0] != 's':
    print('No')
    exit()

# ４方向移動用のリスト
dx = [-1, 0, 1, 0]
dy = [0, -1, 0, 1]

# 探索用の変数
snuke = 'snuke' # 経路の文字列
queue = []        # 幅優先探索のためのキュー
dist = [[-1] * W for _ in range(H)] # 全マスの距離を -1 で初期化

# 初期設定
dist[0][0] = 0    # 開始地点のマスの距離は 0
queue.append([0, 0]) # 開始地点のマスを設定

# 幅優先探索
while queue:
    # キューから先頭のマスの座標を取り出す
    x, y = queue.pop(0)

    # ４方向への探索
    for i in range(4):
        # 移動後のマスの座標
        next_x = x + dx[i]
        next_y = y + dy[i]

        # 移動後のマスが範囲外のとき
        if (next_x < 0 or W <= next_x) or (next_y < 0 or H <= next_y):
            continue

        # 移動後のマスが探索済みのとき
        if dist[next_y][next_x] != -1:
            continue

        # 移動後のマスの文字が違うとき
        if S[next_y][next_x] != snuke[(dist[y][x]+1) % 5]:
            continue

        # 探索できるマスなので開始地点のマスからの距離を更新してキューに追加
        dist[next_y][next_x] = dist[y][x] + 1
        queue.append([next_x, next_y])


# 幅優先探索で右下のマスまで探索できたか判定
if dist[H-1][W-1] != -1:
    print('Yes')
else:
    print('No')

キュー

キューは、データ構造の１つで、先入れ先出し（FIFO：Fisrt In First Out）の規則に従ってデータを管理します。

enqueue でデータを挿入して、dequeue でデータを取り出します。

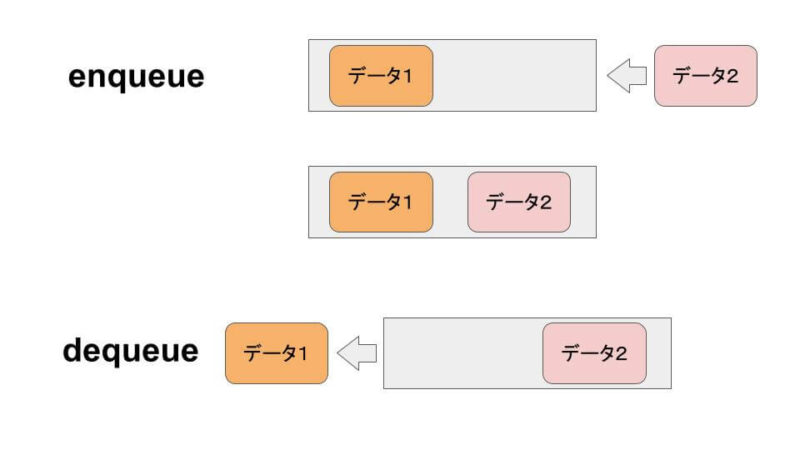
リストをキューとして使うこともできます。

append() でデータを挿入して、pop(0) でデータを取り出します。

queue = []

queue.append('ant')
queue.append('dog')

print(queue)		# => ['ant', 'dog']

a = queue.pop(0)

print(a)			# => ant
print(queue)		# => ['dog']

queue.append('cat')
print(queue)		# => ['dog', 'cat']

【Python】list の使い方

先頭の要素を取り出す処理には時間がかかるので、計算量が多くなる場合は、collections.deque を使えば、リストを使うより高速にキューを実装できます。

from collections import deque

queue = deque()

queue.append('ant')
queue.append('dog')

print(queue)		# => deque(['ant', 'dog'])

a = queue.popleft()

print(a)			# => ant
print(queue)		# => deque(['dog'])
queue.append('cat')
print(queue)		# => deque(['dog', 'cat'])

４方向への探索

現在のマスから４方向へ探索するには、探索用のリストを準備しておくことで簡単に探索することができます。

dx と dy のリストを作り、それを使うことで上下左右の探索を行います。

# 現在のマス。（1, 1）とする
x = 1
y = 1

# ４方向移動用のリスト
dx = [-1, 0, 1, 0]
dy = [0, -1, 0, 1]

# 上下左右の探索
for i in range(4):
    next_x = x + dx[i]
    next_y = y + dy[i]
    print(next_x, next_y)
  
"""実行結果
0 1  # 上
1 0  # 左
2 1  # 下
1 2  # 右
"""

H＼W	0	1	2
0	.	(0, 1)	.
1	(1, 0)	(1, 1)	(1, 2)
2	.	(2, 1)	.

これで現在のマスから４方向への探索ができるようになりました。

移動後のマスを判定

移動後のマスについて次の内容について判定する必要があります。

移動後のマスが、H行W列のグリッド内か
移動後のマスが、まだ探索をしていないマスか
移動後のマスが、現在のマスから見たときに、s → n → u → k → e → s → n → … 順番になる文字か

それを判定しているのが次のコードです。

移動後のマスが、探索すべきマスでないときは、continue で次にスキップしています。

# 移動後のマスが範囲外のとき
if (next_x < 0 or W <= next_x) or (next_y < 0 or H <= next_y):
    continue

# 移動後のマスが探索済みのとき
if dist[next_y][next_x] != -1:
    continue

# 移動後のマスの文字が違うとき
if S[next_y][next_x] != snuke[(dist[y][x]+1) % 5]:
    continue

開始マスからの距離を管理している dist は、‐１で初期化しているので -1 以外のときは探索済みになります。

移動後のマスの文字が snuke のどの文字になるかは、snuke[(dist[y][x]+1) % 5]で判定できます。

dist[y][x] + 1 は、開始地点から現在いるマスまでの距離に１足したものになります。

距離を５で割った余りを求めることで snuke のどの文字かを確認できます。

snuke = 'snuke'
print(snuke[0 % 5])	# => s
print(snuke[1 % 5])	# => n
print(snuke[2 % 5])	# => u
print(snuke[3 % 5])	# => k
print(snuke[4 % 5])	# => e
print(snuke[5 % 5])	# => s
print(snuke[6 % 5])	# => n
print(snuke[7 % 5])	# => u

移動後のマスが探索すべきマスのときは、距離を更新してキューに追加します。

# 探索できるマスなので開始地点のマスからの距離を更新してキューに追加
dist[next_y][next_x] = dist[y][x] + 1
queue .append([next_x, next_y])

これらの処理を queue が空になるまで繰り返します。

探索終了後、探索できたマスの dist には、-1 以外の値が入っています。

# 入力
H, W = map(int, input().split())
S = [input() for _ in range(H)]

# 左上が s でないときは No
if S[0][0] != 's':
    print('No')
    exit()

# ４方向移動用のリスト
dx = [-1, 0, 1, 0]
dy = [0, -1, 0, 1]

# 探索用の変数
snuke = 'snuke' # 経路の文字列
queue = []        # 幅優先探索のためのキュー
dist = [[-1] * W for _ in range(H)] # 全マスの距離を -1 で初期化

# 初期設定
dist[0][0] = 0    # 開始地点のマスの距離は 0
queue.append([0, 0]) # 開始地点のマスを設定

# 幅優先探索
while queue:
    # キューから先頭のマスの座標を取り出す
    x, y = queue.pop(0)

    # ４方向への探索
    for i in range(4):
        # 移動後のマスの座標
        next_x = x + dx[i]
        next_y = y + dy[i]

        # 移動後のマスが範囲外のとき
        if (next_x < 0 or W <= next_x) or (next_y < 0 or H <= next_y):
            continue

        # 移動後のマスが探索済みのとき
        if dist[next_y][next_x] != -1:
            continue

        # 移動後のマスの文字が違うとき
        if S[next_y][next_x] != snuke[(dist[y][x]+1) % 5]:
            continue

        # 探索できるマスなので開始地点のマスからの距離を更新してキューに追加
        dist[next_y][next_x] = dist[y][x] + 1
        queue.append([next_x, next_y])

# 幅優先探索後のdist
print(dist)

"""出力結果
[[0, 1, -1], [-1, 2, 3]]
"""

右下のマス（H – 1、W – 1）の dist が -1 のときは経路が存在せず、-1 以外のときは経路が存在するということになります。

深さ優先探索

深さ優先探索で解いてみます。

深さ優先探索は、スタックを使って探索する方法です。

スタック

スタックは、データ構造の１つで、後入れ先出し（LIFO：Last In First Out）の規則に従ってデータを管理します。

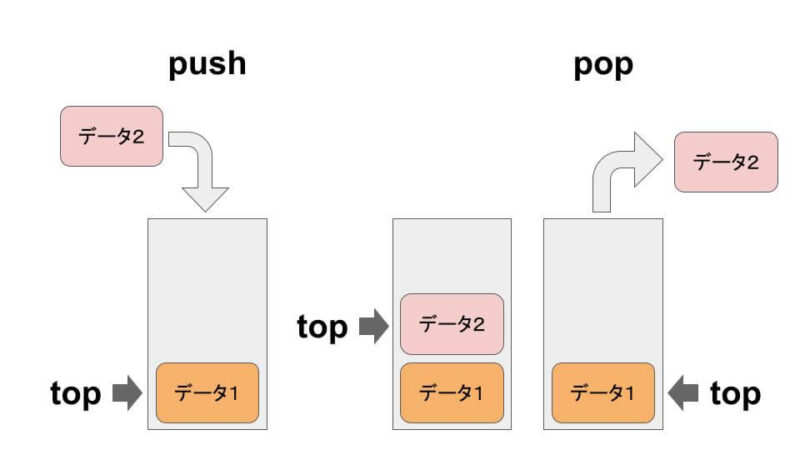
リストをスタックとして使うこともできます。

append() で追加し、pop() で取り出します。

stack = []

stack.append('ant')
stack.append('dog')

print(stack)		# => ['ant', 'dog']

a = stack.pop()

print(a)			# => dog
print(stack)		# => ['ant']

stack.append('cat')
print(stack)		# => ['ant', 'cat']

実装したコードは、次のようになります。

# 入力
H, W = map(int, input().split())
S = [input() for _ in range(H)]

# 左上が s でないときは No
if S[0][0] != 's':
    print('No')
    exit()

# ４方向移動用のリスト
dx = [-1, 0, 1, 0]
dy = [0, -1, 0, 1]

# 探索用の変数
snuke = 'snuke'   # 経路の文字列
stack = []        # 深さ優先探索のためのキュー
dist = [[-1] * W for _ in range(H)] # 全マスの距離を -1 で初期化

# 初期設定
dist[0][0] = 0    # 開始地点のマスの距離は 0
stack.append([0, 0]) # 開始地点のマスを設定

# 深さ優先探索
while stack:
    # キューから先頭のマスの座標を取り出す
    x, y = stack.pop()

    # ４方向への探索
    for i in range(4):
        # 移動後のマスの座標
        next_x = x + dx[i]
        next_y = y + dy[i]

        # 移動後のマスが範囲外のとき
        if (next_x < 0 or W <= next_x) or (next_y < 0 or H <= next_y):
            continue

        # 移動後のマスが探索済みのとき
        if dist[next_y][next_x] != -1:
            continue

        # 移動後のマスの文字が違うとき
        if S[next_y][next_x] != snuke[(dist[y][x]+1) % 5]:
            continue

        # 探索できるマスなので開始地点のマスからの距離を更新してキューに追加
        dist[next_y][next_x] = dist[y][x] + 1
        stack.append([next_x, next_y])


# 深さ優先探索で右下のマスまで探索できたか判定
if dist[H-1][W-1] != -1:
    print('Yes')
else:
    print('No')

変数名を queue から stack に変えましたが、それ以外で変わったのは次の部分です。

pop(0) から pop() に変えました。これでリストから取り出すのが、先頭の要素から最後の要素に変わります。

# キューから先頭のマスの座標を取り出す
x, y = stack.pop()

再帰関数

再帰関数もスタックのように積み上げていきます。

そのため、深さ優先探索は再帰関数で実装することもできます。

超初心者でもわかる再帰関数の基礎！競プロ初心者のためのPython実装ガイド

再帰関数で深さ優先探索を実装したのが、次のコードです。

再帰関数のときは、PyPy より Python の方が実行速度が速いようなので、提出する際の言語に注意してください。

import sys
sys.setrecursionlimit(10**6)

# 入力
H, W = map(int, input().split())
S = [input() for _ in range(H)]

# 左上が s でないときは No
if S[0][0] != 's':
    print('No')
    exit()

# ４方向移動用のリスト
dx = [-1, 0, 1, 0]
dy = [0, -1, 0, 1]

# 探索用の変数
snuke = 'snuke'   # 経路の文字列
seen = [[False] * W for _ in range(H)] # 全マスの未探索である False で初期化

# 深さ優先探索
def dfs(x, y, dist):
    # 右下のマスまで探索できたので終了
    if x == W - 1 and y == H - 1:
        print('Yes')
        exit()

    # ４方向への探索
    for i in range(4):
        # 移動後のマスの座標
        next_x = x + dx[i]
        next_y = y + dy[i]

        # 移動後のマスが範囲外のとき
        if (next_x < 0 or W <= next_x) or (next_y < 0 or H <= next_y):
            continue

        # 移動後のマスが探索済みのとき
        if seen[next_y][next_x]:
            continue

        # 移動後のマスの文字が違うとき
        if S[next_y][next_x] != snuke[(dist+1) % 5]:
            continue

        # 探索できるマスなので探索済みにして探索
        seen[next_y][next_x] = True
        dfs(next_x, next_y, dist + 1)


# 深さ優先探索で右下のマスまで探索できたか判定
dfs(0, 0, 0)

print('No')